Racjonalne kształtowanie konstrukcji hal stalowych wyposażonych w suwnice jest wieloaspektowe. W sytuacji dużego zróżnicowania dostępnych rozwiązań wybór najkorzystniejszego z nich nie jest oczywisty.
Współcześnie najpowszechniej stosowanym typem dźwigu suwnicy w stalowych halach magazynowych lub produkcyjnych są suwnice pomostowe natorowe. Wśród innych typów dźwignic, m.in. suwnic bramowych, półbramowych czy pomostowych podwieszanych, są rozwiązaniem najwygodniejszym w użytkowaniu. Nie wymagają torowiska usytuowanego na poziomie posadzki, nie ograniczają więc wykorzystania jej powierzchni użytkowej. Z tego również względu są bezpieczniejsze w użytkowaniu, ponieważ eliminuje się przynajmniej część zagrożeń, np. ryzyko najechania. Suwnice pomostowe można wykonać jako podwieszane lub natorowe. Wykorzystanie suwnicy w hali wymaga wprowadzenia w jej konstrukcji dodatkowych elementów wsporczych oraz odpowiednich modyfikacji i wzmocnień. W przypadku suwnicy natorowej ingerencja w podstawową konstrukcję hali w celu jej odpowiedniego przygotowania do przejęcia sił przekazywanych z belek podsuwnicowych, po których się porusza dźwignica, jest stosunkowo najmniejsza. Suwnice pomostowe podwieszane wymagają większego stopnia rozbudowy układów nośnych i stężających. Również konstrukcja układów jezdnych tych dźwignic jest znacznie bardziej skomplikowana. Jeśli zatem nie istnieją jakieś szczególne przesłanki zastosowania suwnicy pomostowej podwieszanej (np. gdy szerokość linii roboczej suwnicy jest znacznie mniejsza od rozpiętości nawy hali), to wykorzystuje się suwnice pomostowe natorowe.
>>> Kształtowanie belek podsuwnicowych i przestrzennego układu prętowego – stan graniczny użytkowalności
Suwnice pomostowe natorowe poruszają się po belkach podsuwnicowych opartych na słupach poprzecznych układów nośnych za pośrednictwem krótkich wsporników. Wykorzystanie suwnicy najczęściej w pierwszej kolejności prowadzi do zmiany proporcji hali. Współczesne hale bez suwnic w większości są niskie a szerokie. Suwnica wymaga więcej miejsca w obszarze dachu oraz, w pewnym stopniu, ogranicza rozpiętość nawy. Konstrukcja dźwignicy o większej rozpiętości jest bardziej wymagająca niż konstrukcja ramy o tej samej rozpiętości. W przypadku hal z suwnicami proporcje budynku się zmieniają – budynek jest wyższy i węższy. Na rys. 1 pokazano różne rozwiązania poprzecznych układów nośnych hal z suwnicami: układy ramowe pełnościenne (rys. 1a, 1c) i układy wykorzystujące dźwigary kratownicowe (rys. 1b i 1d); układy podstawowe (rys. 1a, 1b) i przesztywnione w celu zwiększenia bocznej sztywności przechyłowej budynku (rys. 1c, 1d).
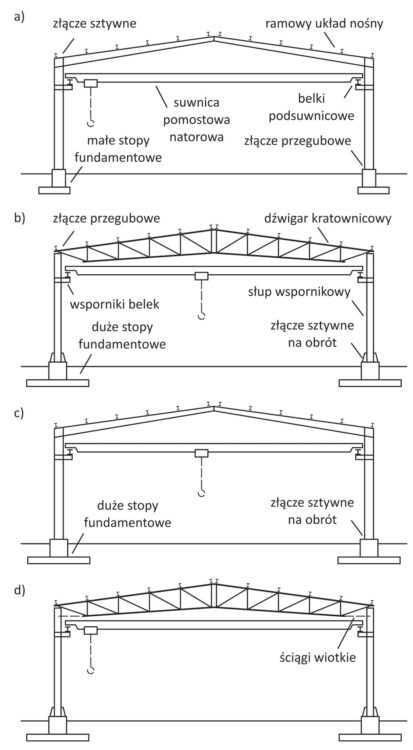
Rys. 1. Podstawowe poprzeczne układy nośne hal z suwnicą: a) rama portalowa oparta przegubowo, b) układ z kratownicą; oraz układy przesztywnione przeciwko przechyłowi poprzecznemu hali: c) rama utwierdzona w fundamencie, d) układ z kratownicą i ściągami wiotkimi na przedłużeniu pasów dolnych
Poprzeczne układy nośne, usytuowane w płaszczyznach ścian szczytowych, często są kształtowane jako indywidualne ustroje słupowo-ryglowe. Przekroje elementów konstrukcji wsporczej ścian szczytowych są mniejsze od przekrojów ram wewnętrznych. W halach z suwnicami, jeśli suwnica ma się poruszać na całej długości przestrzeni użytkowej, to konieczne jest zastosowanie silnego poprzecznego układu nośnego również na obu końcach budynku. Klasycznym rozwiązaniem konstrukcji nośnej w pobliżu ściany szczytowej hali jest zastosowanie układu podwójnego, złożonego z blisko siebie usytuowanych: ramy wewnętrznej, aby oprzeć belki podsuwnicowe, i konstrukcji słupowo-ryglowej, by podeprzeć płaszczyznę ściany szczytowej. Takie rozwiązanie ułatwi w przyszłości ewentualną rozbudowę. Na rys. 2 pokazano przykładowy rzut takiego układu konstrukcyjnego. Oczywiście możliwe jest również odpowiednie wzmocnienie konstrukcji słupowo-ryglowej ściany szczytowej.
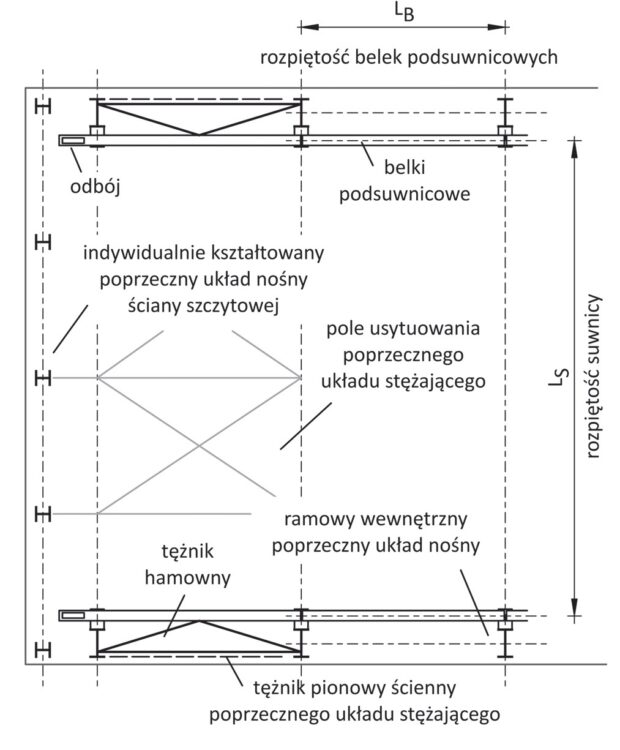
Rys. 2. Rzut przykładowego układu konstrukcyjnego hali z suwnicą

Fot. stock.adobe/DifferR
Oddziaływania przekazywane z suwnicy na belkę podsuwnicową – SGN belki
Suwnica przekazuje na belkę podsuwnicową siły pionowe oraz poziome poprzeczne i podłużne (rys. 3a–3d). Wszystkie siły są oddziaływaniami zmiennymi, choć mamy do czynienia z ciężarem własnym konstrukcji dźwignicy.
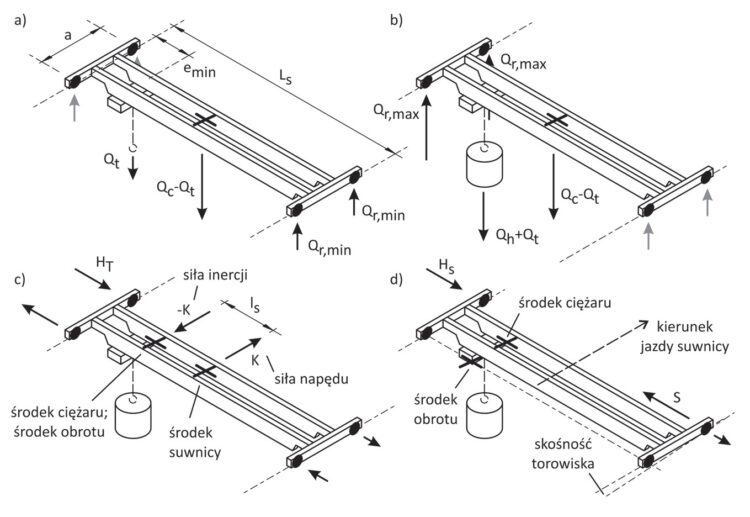
Rys. 3. Oddziaływania przekazywane z suwnicy na belkę podsuwnicową
Suwnica przemieszcza się na długości hali i może nie wystąpić jako obciążenie określonego przęsła belek podsuwnicowych torowiska dźwigu. Z drugiej strony jej ciężar jest dość precyzyjny. Z tego powodu obciążenie przekazywane z suwnicy będzie łączyć cechy oddziaływania zmiennego i pewne cechy oddziaływania stałego. Wartości obliczeniowe oddziaływań przyjmuje się ze współczynnikiem częściowym γQ,sup = 1,35 o wartości górnej właściwej dla oddziaływań stałych. Przy czym wartość dolna tego współczynnika wynosi γQ,inf = 0, jak w przypadku obciążenia zmiennego [1].
Reakcje pionowe przekazywane z suwnicy Qr,max ustalane są na podstawie wartości obliczeniowych oddziaływania zmiennego od ciężaru suwnicy Qc pod pełnym obciążeniem roboczym Qh, z uwzględnieniem współczynników dynamicznych φi, właściwych dla danej sytuacji użytkowania dźwigu. W praktyce projektowej ładunek najczęściej jest podnoszony i opuszczany łagodnie (współczynnik dynamiczny obciążenia dźwigu wynosi φ1=1,1, a ciężaru podnoszonego φ2≈1,05–1,4). Zakres wartości współczynnika dynamicznego wynika z różnej intensywności użytkowania suwnicy. Możliwość gwałtownego zrzucenia ładunku jest przypadkiem rzadszym (współczynnik dynamiczny ciężaru podnoszonego φ3 ≈ 1,0–3,0). Obie sytuacje różnią się znacząco pod względem siły generowanej przez suwnicę i będą wymagały zastosowania konstrukcji wsporczej o innej wielkości. Reakcje maksymalne pod kołami suwnicy Qr,max ustala się przy założeniu, że wózek suwnicy wraz z ciężarem podnoszonym znajduje się w położeniu skrajnym emin (rys. 3b).
Ustalanie reakcji w płaszczyźnie poziomej jest bardziej wymagające głównie dlatego, że jest kilkuetapowe oraz należy sprawdzić kilka modeli normowych powstawania tych sił. Siły boczne ustala się na podstawie reakcji pionowych, ustalanych ponownie, przy zmienionej wartości współczynnika dynamicznego φ4 = 1,0. W normie [1] zaproponowano trzy mechanizmy generowania przez suwnicę oddziaływań w płaszczyźnie poziomej. Są to oddziaływania od: przyspieszenia suwnicy wzdłuż torowiska, imperfekcji zukosowania torowiska suwnicy oraz przyspieszenia wózka suwnicy poprzecznie do torowiska. W praktyce projektowej jako miarodajne uznaje się dwie pierwsze sytuacje.
Siły od przyspieszenia suwnicy określane są dwuetapowo. W pierwszym etapie ustala się normową wartość sił przyspieszenia suwnicy K. Wartość normowa przyjmowana jest jako maksymalna możliwa siła tarcia pod kołami napędowymi, przy założeniu pełnego odciążenia suwnicy (reakcje minimalne Qr,min – rys. 3a). Model normowy przyjmuje asekuracyjne założenie, że siła napędu jest tak duża, jak to tylko możliwe, a to niezasadnie generuje znaczne siły poziome przekazywane na belkę podsuwnicową. W rzeczywistości siły napędu są znacznie mniejsze i mogłyby być podstawą do dalszych obliczeń – jeżeli producent suwnicy podałby ich realne wartości w specyfikacji dźwigu. Z niejasnych powodów jest to rzadka praktyka, a specyfikacje najczęściej zawierają wartości ustalane zgodnie z normą. W drugim etapie obliczeń wyznacza się maksymalne ramię ls między parą sił napędu K i inercji suwnicy (-K). Moment siły inercji jest największy, gdy wózek znajduje się w położeniu skrajnym, a suwnica jest w pełni dociążona (rys. 3c). Suwnica próbuje się obrócić w płaszczyźnie torowiska. Zapobiegają temu siły poziome poprzeczne HT oddziałujące na ramieniu równym rozstawowi jej kół a. Im większy jest rozstaw kół suwnicy, tym siły poziome poprzeczne przekazywane na belkę podsuwnicową są mniejsze. Z tego powodu w konstrukcjach suwnic natorowych wielu producentów widoczna jest ta korzystna cecha, gdy koła są rozsunięte na dość dużą odległość. Rozstaw kół suwnicy jest jednym z parametrów najistotniej wpływających na wartości sił bocznych przekazywanych z suwnicy na belkę podsuwnicową. Oddziaływania poziome od sił przyspieszenia suwnicy zwiększa się współczynnikiem dynamicznym 1,0 ≤ φ5 ≤ 1,5. Zakres współczynnika jest szeroki i dotyczy współczesnych suwnic, w których siły zmieniają się łagodnie. Wartość tego współczynnika może podać producent suwnicy. Jeśli nie, to najczęściej przyjmuje się asekuracyjnie wartość górną.
W przypadku drugiego modelu przyjmuje się założenie, że suwnica pod pełnym obciążeniem, gdy wózek suwnicy jest w położeniu skrajnym, w trakcie jazdy uderza bocznie kołem prowadzącym w skośnie ustawiony tor (koło prowadzące – koło z przodu do kierunku jazdy). Podana w normie skośność toru jest umowna i ma reprezentować w obliczeniach niedokładność wykonania torowiska. Podobnie jak w poprzednim modelu normowym, tak i w tym przypadku wartości obliczeniowe wydają się być przyjęte asekuracyjnie. Skośność torowiska, jeśli nie wykonuje się dokładniejszych obliczeń, przyjmuje się o wartości 0,015. W praktyce wykonawczej taka niedokładność jest zupełnie nierealna. Uderzenie obrzeżem koła w skośnie położoną szynę torowiska generuje siłę destabilizującą S. Suwnica próbuje się obrócić względem punktu leżącego na przecięciu osi tylnej i osi wzdłużnej przechodzącej przez środek ciężkości suwnicy. Obrót suwnicy ograniczają siły poziome poprzeczne Hs powstające na obrzeżach kół przedniej osi i oddziałujące na suwnicę z ramieniem równym rozstawowi jej kół a (rys. 3d).
Zarówno siły boczne od przyspieszenia suwnicy HT oraz od zukosowania toru suwnicy Hs oddziałują na ramieniu skrętnym odliczonym od wierzchu szyny do środka zginania przekroju. Skutkiem działania sił jest zginanie boczne belki, a mimośrodu – skręcanie. Po uwzględnieniu skręcania zdwaja się wytężenie belki od działania sił bocznych.
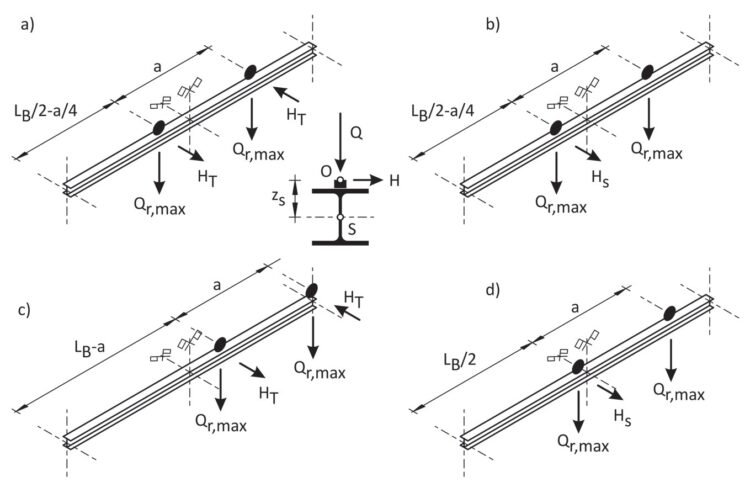
Rys. 4. Przypadki ustawienia suwnicy przy weryfikacji stanów granicznych belki podsuwnicowej
Gdy belka podsuwnicowa jest jednoprzęsłowa (najczęściej stosowane rozwiązanie), suwnicę ustawia się przednim kołem w pozycji x1 = LB⁄2 – a⁄4. W tym położeniu suwnicy, gdy rozstaw kół nie przekracza wartości a⁄LB ≤ 0,586, uzyskuje się maksymalne wytężenie belki od zginania w płaszczyźnie silnej (rys. 4a i 4b). Niestety wielu projektantów analizuje belkę podsuwnicową wyłącznie przy tym ustawieniu suwnicy. Przyjmują, że obciążeniem wiodącym belki na pewno jest obciążenie pionowe Qr,max i uzupełniają obciążenie pionowe o siły poziome poprzeczne. Obciążenie boczne jest często wyłącznie traktowane jako dopełniające. Takie założenie jest nieprawidłowe. Belka podsuwnicowa jest konstrukcją o specyficznym sposobie obciążenia – jest ona zginana dwukierunkowo i skręcana (My,Ed, Mz,Ed, BEd), o mniej więcej równym udziale wytężenia od każdej z tych sił. W tym samym stopniu przekrój konstrukcji wytęża zginanie w płaszczyźnie silnej, zginanie boczne czy bimoment wywołany skręceniem. Jest to mało intuicyjne, ponieważ oddziaływania pionowe są większe od oddziaływań bocznych. Warto jednak mieć świadomość, że skutkiem tego samego oddziaływania bocznego H są dwie składowe wewnętrznego stanu obciążenia Mz,Ed i BEd. Wpływ tego obciążenia na wytężenie belki może być decydujący. Maksymalne wytężenie od zginania bocznego i od bimomentu w przypadku sił bocznych od przyspieszenia suwnicy uzyskuje się, gdy suwnica jest w położeniu skrajnym x1 = LB – a (rys. 4c), a w przypadku sił zukosowania, gdy suwnica stoi przednim kołem na środku belki x1 = LB⁄2 (rys. 4d).
Problematyczne jest to, że maksymalizację każdej ze składowych wewnętrznego stanu obciążenia belki uzyskuje się przy innym położeniu suwnicy. Konieczne jest zatem sprawdzenie czterech przypadków, w których kolejno maksymalizuje się wytężenie od sił albo pionowych, albo bocznych, a pozostałe siły przyjmuje się jako dopełniające.
Warunek stanu granicznego nośności belki podsuwnicowej weryfikuje się przy założeniu utraty stateczności oraz sprężystego stanu naprężeń normalnych, niezależnie od klasy przekroju:
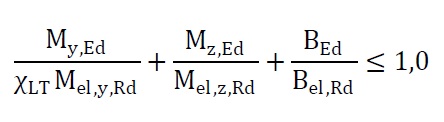
O ile weryfikacja warunku nośności według [2] sama w sobie jest dość prosta, o tyle kłopotliwa jest analiza równowagi statycznej belki przy skręcaniu. W poradnikach inżynierskich [3, 4] omówiono zaledwie wybrane przypadki analizy belek według teorii prętów cienkościennych Własowa. Wzory analityczne dotyczące przypadków bardziej wymagających można znaleźć raczej w opracowaniach o charakterze naukowo-badawczym [5]. Analiza statyczna belek skręcanych staje się szczególnie trudna, gdy belkę podsuwnicową krępuje bocznie układ zastrzałów lub stężenie kratownicowe. Takie rozwiązania można znaleźć wyłącznie w rzadkich pracach badawczych dotyczących bezpośrednio zagadnień zachowania się belek podsuwnicowych [6]. W obliczeniach statycznych można wykorzystać oprogramowanie numeryczne. Przy czym dopiero w ostatnim czasie pojawiły się na rynku programy z elementami skończonymi o siedmiu stopniach swobody w węźle, umożliwiające uwzględnienie spaczenia. Programy z elementami skończonymi o sześciu stopniach swobody w węźle są nieadekwatne do analizy tego typu problemów.
Złożoność obciążenia przekazywanego z suwnicy przekłada się na dobór rozwiązania konstrukcyjnego, zarówno przekroju poprzecznego, jak i schematu statycznego belki. W przypadku belki podsuwnicowej istotne jest, aby przy racjonalnym projektowaniu z równą uwagą rozważać schemat statyczny w dwóch płaszczyznach – pionowej i bocznej.
Belki podsuwnicowe – rozwiązania konstrukcyjne
Podstawowym przekrojem poprzecznym stalowych belek podsuwnicowych jest dwuteownik szerokostopowy HEA lub HEB (rys. 5a). Dwuteowniki walcowane początkowo zostały opracowane jako kształtowniki belek zginanych jednokierunkowo (IPN). Ich wąski, lecz wysoki przekrój był jednak zupełnie niewłaściwy w przypadku belki, w której, poza zginaniem w płaszczyźnie silnej, występowały inne składowe stanu obciążenia. Dwuteownik szerokostopowy, o proporcjach zbliżonych do kwadratu, został opracowany na wypadek wystąpienia w belce właśnie takiego złożonego stanu sił: zginania w płaszczyźnie silnej, zginania bocznego i skręcania.
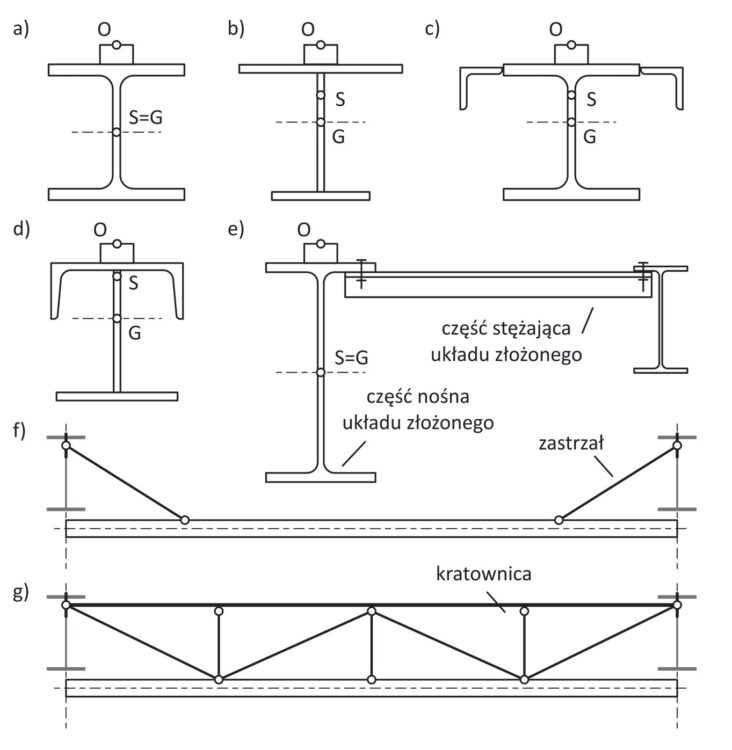
Rys. 5. Rozwiązania przekrojów poprzecznych belek podsuwnicowych: a) kształtownik dwuteowy szerokostopowy, b–d) przekroje monosymetryczne, e–g) układy złożone z dwóch konstrukcji: nośnej i stężającej
Dodatkowo ma on większą nośność zwichrzeniową, gdy belka jest długa i ma duży rozstaw podpór przeciwskrętnych. Ze względu na specyfikę podparcia oraz sposób obciążenia belka podsuwnicowa jest wrażliwa na jednoczesne wystąpienie wszystkich tych problemów.
Rozwiązanie podstawowe z wykorzystaniem dwuteownika szerokostopowego ma zalety wynikające głównie z pewnej prostoty i możliwości zastosowania gotowego kształtownika, jednak jest ono nieoptymalne. Wskutek złożoności stanu obciążenia uzyskuje się silną dysproporcję wytężenia pasów górnego i dolnego. Różnice naprężeń w pasach górnym i dolnym są trzykrotne, co wskazuje na zupełne niedopasowanie symetrycznego kształtu przekroju poprzecznego do asymetrycznego obciążenia. Jest to podejście nieefektywne i prowadzi do konieczności zużycia większej ilości materiału. Szczególnie w odniesieniu do belki o przekroju monosymetrycznym lub belki o układzie złożonym (belka uzupełniona boczną konstrukcją stężającą). Przekrój dwuteowy szerokostopowy jest zatem stosowany w przypadku suwnic o mniejszym udźwigu i gdy rozpiętość belki podsuwnicowej nie jest duża.
Przekrój dwuteowy szerokostopowy najczęściej łączy się z jednoprzęsłowym schematem statycznym belki, zarówno w płaszczyźnie pionowej, jak i bocznej. Schemat jednoprzęsłowy jest stosowany najczęściej i dlatego można go również potraktować jako podstawowy wariant rozwiązania konstrukcyjnego.
Zobacz też:
- Projektowanie układów kratowych hal z kształtowników zamkniętych
- Kształtowniki zamknięte w projektowaniu układów kratowych hal
- Konstrukcje stalowe hal wielkopowierzchniowych
- Hale pneumatyczne od A do Z
- Produkty budowlane
W przypadku belek podsuwnicowych o większym obciążeniu lub rozpiętości warto jest rozważyć rozwiązanie o większym stopniu skomplikowania kształtu przekroju poprzecznego lub schematu statycznego w płaszczyznach pionowej lub bocznej. Zwiększone obciążenie graniczne i sztywność belki podsuwnicowej można zapewnić na kilka sposobów.
Od wielu dziesięcioleci na belki podsuwnicowe stosuje się przekroje monosymetryczne. Najczęściej są one stosowane w jednym z trzech wariantów rozwiązania. Pierwszym kształtem monosymetrycznym jest blachownica dwuteowa z poszerzonym pasem górnym i zwężonym pasem dolnym (rys. 5b). Pasy można zróżnicować przez zmianę ich grubości, jednak to rozwiązanie jest mniej efektywne i dlatego rzadziej stosowane. W rozwiązaniach starszych dwuteownik walcowany uzupełniano dwoma kątownikami (rys. 5c). Ten rodzaj przekroju współcześnie zastępuje się raczej blachownicą dwuteową, której pas górny wykonuje się z ceownika walcowanego (rys. 5d). To rozwiązanie zapewnia najlepsze dopasowanie rozkładu powierzchni przekroju poprzecznego względem sposobu obciążenia elementu.
Efektywność rozwiązań, w których pas górny jest rozbudowany względem pasa dolnego, wynika z połączenia kilku korzystnych czynników. Po pierwsze, przekroje te mają zwiększoną sztywność i nośność przy zginaniu bocznym i przy skręcaniu. Po drugie, środek zginania jest położony blisko górnego pasa, a nie w środku przekroju, jak w przypadku dwuteowników bisymetrycznych. Siła pozioma poprzeczna HT oddziałuje na belkę z kilkakrotnie mniejszym mimośrodem skrętnym. Przy odpowiednio dobranych proporcjach części przekroju naprężenia w obu pasach się wyrównują i są mniejsze, a materiał jest wykorzystany efektywnie. Przekroje monosymetryczne stosowane są w połączeniu z jednoprzęsłowym schematem statycznym.
Przy rozważaniu możliwej zmiany schematu statycznego można rozróżnić dwa podejścia – pierwsze polegające na uzupełnieniu belki dodatkowym prętowym układem konstrukcyjnym (rozwiązanie złożone, rys. 5e–g), drugie polegające na zmianie sposobu skrępowania belki podsuwnicowej, ale bez zastosowania dodatkowych prętowych podukładów stężających.
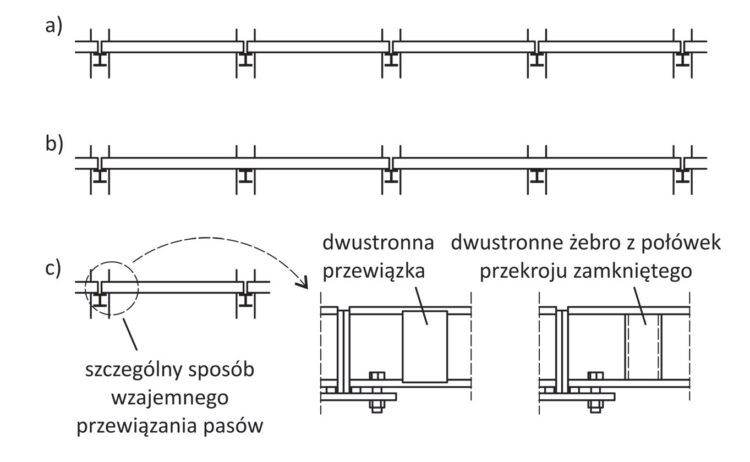
Rys. 6. Schematy statyczne belek podsuwnicowych
Najprostszym sposobem zwiększenia obciążenia granicznego i sztywności belki w obu płaszczyznach jest zmiana schematu statycznego jednoprzęsłowego (rys. 6a) na dwuprzęsłowy (rys. 6b). Wybór możliwych modyfikacji schematu statycznego w płaszczyźnie pionowej jest niestety dość ograniczony. W praktyce projektowej w większym stopniu różnicuje się schematy statyczne belek podsuwnicowych w płaszczyźnie bocznej. Zmiana schematu jednoprzęsłowego na dwuprzęsłowy jest niemal zupełnie bezproblemowa, jednak ma swoje ograniczenia. Schemat dwuprzęsłowy wymaga parzystej liczby przęseł hali, ograniczenia długości przęsła poniżej 6 m (długość maks. prefabrykatu to 12 m) oraz wymusza zastosowanie przekroju bisymetrycznego (wystąpienie ujemnego momentu zginającego nad podporą wewnętrzną). Geometria, w której kolejne przęsła belki podsuwnicowej usytuowane są współosiowo i są o stałym przekroju, pozwala się zastanowić nad wyborem układu wieloprzęsłowego ciągłego. Niestety, wykorzystanie tego schematu jest istotnie ograniczone ze względu na problemy zmęczenia śrub połączeń doczołowych. W przypadku belki dwuprzęsłowej przęsła jednego prefabrykatu łączą się poprzez ciągłość materiału, a złącza doczołowe śrubowe w ogóle nie są wykorzystywane. Dlatego też, jeśli w halach z suwnicami stosuje się układy ciągłe, to niemal wyłącznie dwuprzęsłowe. Wybór rozwiązania dwuprzęsłowego należy traktować jako rozwiązanie bardzo racjonalne.
>>> Budynki z płyt warstwowych – okresowe kontrole stanu technicznego
>>> Konstrukcja hali stalowej – rozwiązania
Najskuteczniejszym sposobem zwiększenia sztywności bocznej giętnej i skrętnej belki podsuwnicowej jest zastosowanie układów złożonych. Opisane zostaną dwa rozwiązania układów dwuczęściowych, złożonych z części usytuowanej pionowo – nośnej, i bocznie – stężającej. Dodatkowy układ stężający znacząco zmniejsza zarówno deformację giętną boczną, jak i skrętną. Rozwiązaniem o dużej sztywności, wymagającym zwiększenia ilości materiału i robocizny, jest uzupełnienie układu nośnego stężeniem kratownicowym usytuowanym w płaszczyźnie pasa górnego belki (rys. 5e i 5g). W przypadku tego rozwiązania stosuje się przekrój belki podsuwnicowej właściwy w przypadku belek zginanych płasko (kształtowniki IPE, wąskie a wysokie blachownice). Obie części tej złożonej konstrukcji niemal w całości przejmują składowe obciążenia z suwnicy oddziałujące w ich płaszczyznach. Rozwiązanie to jest uzasadnione w przypadku belek podsuwnicowych o dużych rozpiętościach lub o dużym obciążeniu. Przy oddziaływaniach o średniej wielkości warto jest rozważyć jedno z rozwiązań pośrednich. Rozwiązaniem mało rozpoznanym, jednak wyjątkowo skutecznym, jest zastosowanie zastrzałów łączących skośnie pasy górne belki podsuwnicowej ze słupami ram poprzecznego układu nośnego (rys. 5f). Jest to w pewnym stopniu zredukowana wersja opisanego wcześniej wzmocnienia przy użyciu kratownicy. Podobnie jak w przypadku belki z kratownicą jest to rozwiązanie dwuczęściowe, złożone z części nośnej i stężającej. Przy czym zamiast układu bocznego wieloprzeponowego, w którym kolejne przepony łączą się w jedną kratownicę, belkę usztywnia się bocznie przy użyciu dwóch odseparowanych przepon, usytuowanych na dwóch końcach belek. Pod względem sposobu skrępowania belki zastrzał pełni funkcję przepony, ponieważ krępuje wzajemne przesuwy dwóch węzłów. Jest to rozwiązanie proste pod względem montażowym. Konstrukcję podstawową uzupełnia się zaledwie dwoma prętami, najczęściej o niewielkim przekroju kątowym.
Ostatnią modyfikacją schematu statycznego belki w jej płaszczyźnie bocznej jest zastosowanie elementów przypodporowych krępujących deformację spaczenia. Jest to rozwiązanie mało rozpowszechnione w praktyce projektowej, chociaż prawie dwukrotnie podnosi sztywność i nośność skrętną. Polega ono na wzajemnym przewiązaniu dwóch pasów dwuteownika belki podsuwnicowej (rys. 6c). Podobnie jak w przypadku belki z zastrzałami rozwiązanie jest proste pod względem konstrukcyjnym. Skrępowanie spaczenia przekrojów przypodporowych uzyskuje się przez zastosowanie przewiązek lub żeber o przekroju zamkniętym. Dodatkowe elementy są wykonywane jako część prefabrykatu belki podsuwnicowej i nie utrudniają montażu (są umieszczane w pobliżu podpór, a nie w osi podpór)
dr inż. Łukasz Supeł
Politechnika Łódzka
Katedra Mechaniki Konstrukcji
Literatura
- PN-EN 1991-3 Eurokod 1 – Oddziaływania na konstrukcje – Część 3: Oddziaływania wywołane dźwignicami i maszynami.
- PN-EN 1993-1-1 Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-1: Reguły ogólne i reguły dla budynków.
- Opracowanie zbiorowe, Poradnik inżyniera i technika budowlanego, tom 3, Arkady, Warszawa 1998.
- J. Żmuda, Konstrukcje wsporcze dźwignic, Wydawnictwo Naukowe PWN, Warszawa 2013.
- S. Weiss, K. Gergovich, Podstawy mechaniki pręta cienkościennego, Wydawnictwo Politechniki Krakowskiej, Kraków 1973.
- I. Kowalczyk, Analiza porównawcza rozwiązań belek podsuwnicowych z wykorzystaniem teorii skręcanych prętów cienkościennych Własowa, praca dyplomowa magisterska, Wydział Budownictwa, Architektury i Inżynierii Środowiska, Politechnika Łódzka, Łódź 2022.