Celem artykułu jest zaproponowanie udoskonalonego modelu toru na kolejowym obiekcie mostowym z uwzględnieniem parametrów eksploatacyjnych dotychczas pomijanych, które wpływają na zmianę stanu naprężeń w podsypce kolejowej, a tym samym – na wielkość oddziaływań tor–most.
Wraz z modernizacją polskiej sieci kolejowej dokonuje się wymiany obiektów mostowych. Obiekty starsze, z ograniczeniem prędkości do 120 km/h, na których tor jest ułożony na mostownicach, stanowiące ponad 40% obiektów, zastępowane są podsypkowymi. Podnoszona jest prędkość projektowa nawet do 200 km/h, a także zwiększane są długości przęseł. W związku z tym pojawia się pytanie o konieczność zastosowania przyrządów wyrównawczych. Ogólnie uważa się, że stanowią one słaby element nawierzchni oraz że wymuszają dodatkowe utrzymanie. Ponadto zgodnie z wytycznymi PKP PLK S.A. zasadność ich zastosowania należy wykazać. Jednakże brakuje ścisłych danych w odniesieniu do rzeczywistej pracy toru bezstykowego na obiektach oraz modeli opisujących oddziaływania tor-przęsło obiektu. Wymagania Eurokodu 1 [1], z modelem sprężysto-plastycznym podsypki, prowadzą do przeszacowania wielkości oddziaływań.
Cel i sposób analizy oraz opis obiektu mostowego
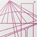
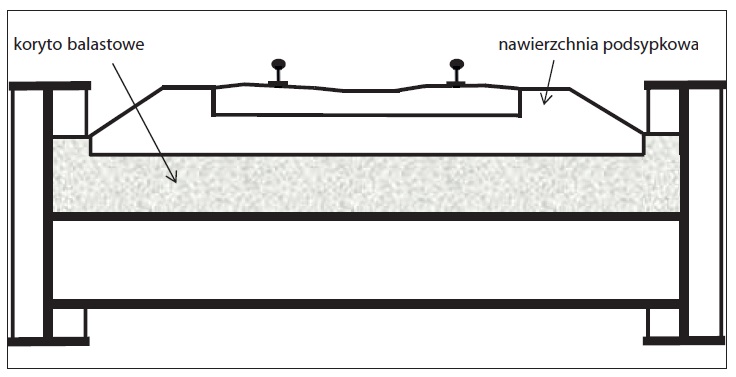
Celem autorów jest zaproponowanie udoskonalonego modelu toru na obiekcie mostowym z uwzględnieniem parametrów eksploatacyjnych dotychczas pomijanych, tj. m.in. drgań w wyniku jazdy pociągów, które wpływają na zmianę stanu naprężeń w podsypce kolejowej, a tym samym – na wielkość oddziaływań tor–most. Jako obiekt studialny przyjęto most nad rzeką Wisłoka w ciągu linii E30. Schemat statyczny mostu i łożyskowania przęseł przedstawiono na rys. 1, a widok ogólny obiektu pokazano na fot.

Fot. Widok ogólny mostu nad rzeką Wisłoka w pobliżu miasta Dębica na linii E30
Rys. 1. Schemat statyczny analizowanego obiektu nad rzeką Wisłoka
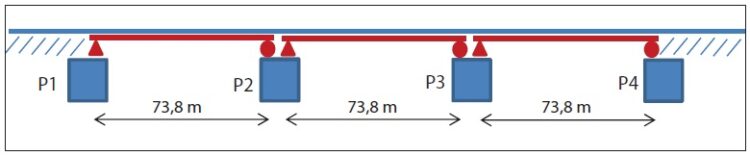
Analizowany obiekt ma konstrukcję stalową przęseł – dotyczy to zarówno płyty pomostu, jak i łuków. Pomiędzy dźwigarami stalowymi umiejscowione jest żelbetowe koryto balastowe, na którym znajduje się mata wibroizolacyjna o grubości 25 mm oraz kolejowa nawierzchnia podsypkowa o grubości warstwy tłucznia 35 cm, składająca się z szyn 60E1 i podkładów PS-94M z przytwierdzeniami SB-4. Przekrój poprzeczny konstrukcji przedstawiono na rys. 2.
Rys. 2. Przekrój poprzeczny analizowanego mostu [2]
Analizowany obiekt mostowy, składający się z trzech przęseł pracujących jak niezależne belki wolno podparte, ma długość 222 m. Dla pewnego uproszczenia analizy w artykule pomięto czwarte przęsło występujące od strony Dębicy, które jest znacznie krótsze (poniżej 15 m rozpiętości) oraz jest wykonane jako żelbetowe.
Przyjęcie obciążenia termicznego
Obciążenie termiczne przyjęto na podstawie obowiązującego normatywu [3] oraz zastosowano tzw. temperaturę efektywną dla typu obiektu nr 1 (most o konstrukcji stalowej według [3]). Wysokość obiektu nad poziomem morza znajdującego się w obszarze Dębicy wynosi 190 m. Zgodnie z mapą izoterm dla Polski temperatura maksymalna wynosi +35°C, a temperatura minimalna –30°C. Według wspomnianego Eurokodu maksymalna temperatura efektywna mostu wynosi: +35°C + 16°C = +51°C, natomiast minimalna temperatura efektywna wynosi: –30°C – 3°C = –33°C. Przy założeniu, że temperatura odniesienia jest zgodna z tzw. temperaturą neutralną szyn, w której następuje przytwierdzenie szyn do podkładów – tj. znajduje się w przedziale od +15°C do +30°C, otrzymuje się następujące obliczeniowe przyrosty temperatury efektywnej mostu przy najbardziej niekorzystnym układzie temperatur:
- warunki letnie: +51°C – 15°C = +36°C (przyrost temperatury mostu),
- warunki zimowe: –33°C – 30°C = –63°C (spadek temperatury mostu).
Wskazane wartości temperatury stanowią „ramy” obliczeniowe zmiany temperatury efektywnej obiektu.
Największa dopuszczalna różnica temperatury pomiędzy temperaturą szyn a temperaturą efektywną mostu zgodnie z [3] wynosi ±20°C. Biorąc pod uwagę przedstawione wymagania, obliczono kombinacje obciążenia termicznego obiektu oraz szyn toru bezstykowego, co pokazano przy prezentowanych przypadkach obliczeń. Przyjęto współczynnik rozszerzalności termicznej szyn i mostu jako: αsz = 1,15E–5 1/°C oraz αm = 1,10E–5 1/°C.
W celu weryfikacji wyznaczonych wartości przemieszczeń wzdłużnych przęseł obiektu porównano wyniki obliczeń w modelu 3D [2] z obliczeniami z wykorzystaniem temperatury efektywnej. Stwierdzono dobrą zbieżność wyników, co ilustruje rys. 3.
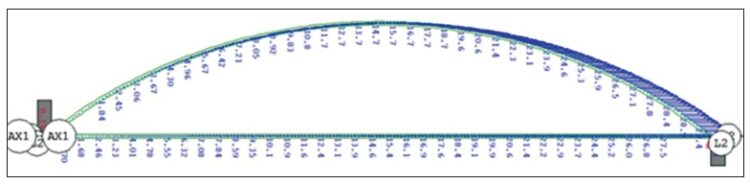
Rys. 3. Wydłużenie przęsła mostu przy równomiernym przyroście temperatury wszystkich elementów mostu o 40°C [2] wynosi 29,4 mm. Analogiczne wydłużenie z wykorzystaniem przyrostu temperatury efektywnej +40°C: 73,8 m x 40°C x 1,10E–5 1/°C = 32,5 mm. Dla wyznaczonego maksymalnego przyrostu temperatury według Eurokodu [3], czyli dla 36°C, wydłużenie przęsła wynosi 29,3 mm
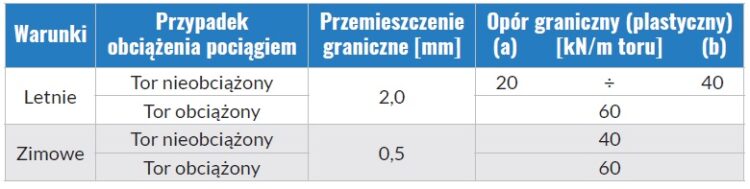
Tab. 1. Opory wzdłużne toru [kN/m toru] według Eurokodu [1]
>>> Parametry elektryczne torowisk zabudowanych – konduktancja toru
>>> Parametry elektryczne torowisk zabudowanych – rezystancja toru
>>> Zielone torowiska podstawą nowoczesnej infrastruktury miejskiej
Parametry mechaniczne podsypki
Z uwagi na współpracę obiektu mostowego z nawierzchnią kolejową w kierunku wzdłużnym bardzo istotny jest tzw. opór wzdłużny toru na jednostkę długości toru. Zgodnie z Eurokodem [1] zastępczy opór wzdłużny toru (obejmujący opór przytwierdzeń oraz podkładów posadowionych w podsypce) przyjmuje się jako sprężysto-plastyczny zgodnie z tab. 1 odpowiednio dla warunków zimowych i letnich oraz w zależności od tego, czy tor jest obciążony pociągiem, czy nie (rys. 4). Opór wzdłużny toru o charakterystyce sprężysto-plastycznej jest pewną aproksymacją oporów wzdłużnych toru, której wykorzystanie daje wyniki obliczeń oddziaływań pomiędzy mostem a torem po stronie bezpiecznej.
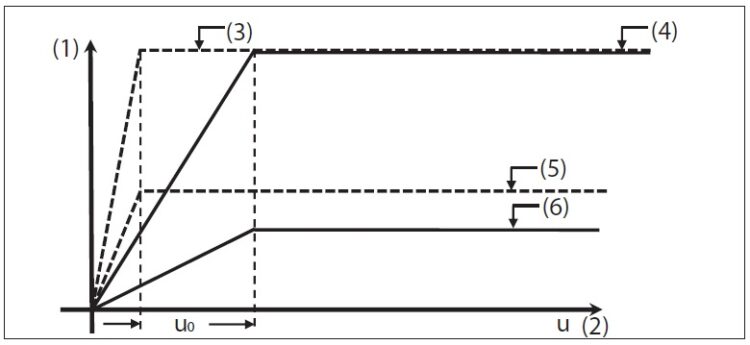
Rys. 4. Sprężysto-plastyczny model oporu wzdłużnego toru (przytwierdzenie + podkład posadowiony
w podsypce) [1]: 1 – opór wzdłużny [kN/m toru], 2 – przemieszczenie wzdłużne szyny [m], 3 – opór graniczny
w warunkach zimowych przy obciążeniu pociągiem, 4 – jw. dla warunków letnich, 5 – opór graniczny w warunkach zimowych bez obciążenia pociągiem, 6 – jw. dla warunków letnich, u0 – przemieszczenie graniczne
Takie ujęcie pracy oporu wzdłużnego toru oznacza, że po przekroczeniu pewnego niewielkiego przemieszczenia granicznego (tj. 2,0 mm oraz 0,5 mm, odpowiednio dla warunków letnich i zimowych) opór wzdłużny przechodzi w stan plastyczny. Dzieje się to prawie na całej długości przęsła, gdyż zmiana jego temperatury np. o 6°C już na długości zaledwie 30 m od łożyska nieruchomego powoduje wydłużenie przęsła o wartość 2,0 mm i tym samym przejście oporu wzdłużnego w stan graniczny. Dla analizowanego obiektu mostowego – o rozpiętości przęsła 73,80 m – oznacza to, że już 60% oporu wzdłużnego będzie pracowało w stanie granicznym (plastycznym). Zmiana temperatury obiektu mostowego następuje dość szybko, np. według [4, 8] pojawiają się przyrosty temperatury rzędu 4–5°C/godz. W przypadku warunków zimowych, kiedy przemieszczenie graniczne wynosi 0,5 mm, przy zmianach temperatury tego rzędu 90% oporu wzdłużnego przechodzi w stan graniczny. Wskutek zastosowania modelu sprężysto-plastycznego oporu wzdłużnego przy dobowych wahaniach temperatury przekraczających kilkanaście stopni można stwierdzić, że prawie na całej długości przęseł mostu obserwuje się pracę podsypki w stanie granicznym zarówno w warunkach letnich, jak i zimowych.
Ujęcie charakterystyki oporu wzdłużnego w postaci modelu sprężysto-plastycznego z pewnością prowadzi do przeszacowania oddziaływań most–tor w kierunku wzdłużnym. Charakterystyki oporów wzdłużnych (r), zwłaszcza podsypki, mogą być aproksymowane innymi funkcjami, np. [5, 6, 10]:
r = α uβ (1)
r = u/(α u + β) (2)
gdzie:
α, β – współczynniki aproksymacji,
u – przemieszczenie wzdłużne (szyny lub podkładu w podsypce).
Przykłady aproksymacji oporów wzdłużnych podkładu w podsypce wykonanych przez autorów z wykorzystaniem powyższych funkcji pokazano na rys. 5 [7].
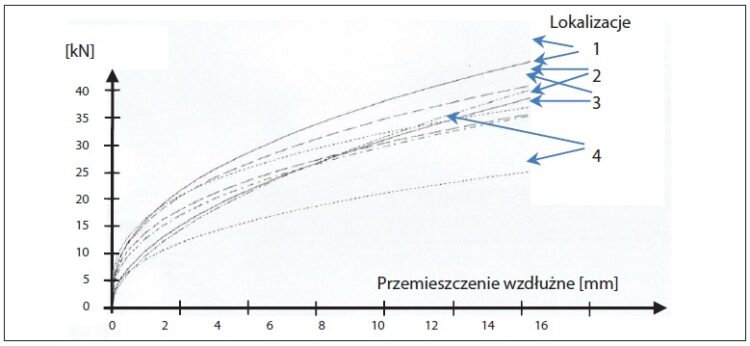
Rys. 5. Wyniki badań oporu wzdłużnego podkładów w podsypce tłuczniowej [7]. Pokazano krzywe odpowiadające oporowi po lewej i prawej stronie toru
Pomiary zostały wykonane w kilku lokalizacjach: 1) na stacji Kraków Główny (nawierzchnia: szyny S60, podkłady drewniane, tor nowy oddany do eksploatacji); 2) na linii Kraków–Medyka, km 3.920, szyny S60, podkłady drewniane; 3) na linii Kraków Mielniki–Gaj, km 4.870, szyny S60, podkłady strunobetonowe – badania na torach nr 1 i nr 2; 4) na linii Kraków–Medyka, tor nr 1, km 1.760, szyny S60, podkłady drewniane z drewna azobe, tor nr 2, km 1.950, szyny S60, podkłady drewniane z drewna azobe. Opory wzdłużne wyznaczono po zdjęciu przytwierdzeń, uniesieniu szyn oraz z wykorzystaniem pomiaru siłownikiem hydraulicznym, który „rozpychał” sąsiednie podkłady. Przedstawione na rys. 5 krzywe były typu (1) oraz posiadały współczynniki korelacji pokazane w tab. 2.
Tab. 2. Współczynniki równania aproksymacyjnego (1) oraz współczynniki korelacji (R) z danymi pomiarowymi
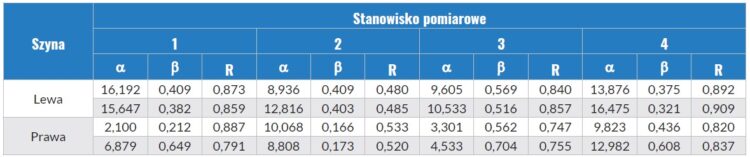
Uwaga: w wierszach górnych i dolnych dla danej szyny pokazano aproksymacje dla pomiaru dwóch sąsiednich podkładów.
Dla rozważań zawartych w artykule najważniejsze są wyniki uzyskane na stanowisku nr 3, ponieważ typ nawierzchni był taki sam, jak na analizowanym moście (szyny S60, które zastąpiono szynami 60E1, podkłady strunobetonowe). Przykłady krzywych doświadczalnych uzyskane na stanowisku nr 3 pokazano na rys. 6 i 7.
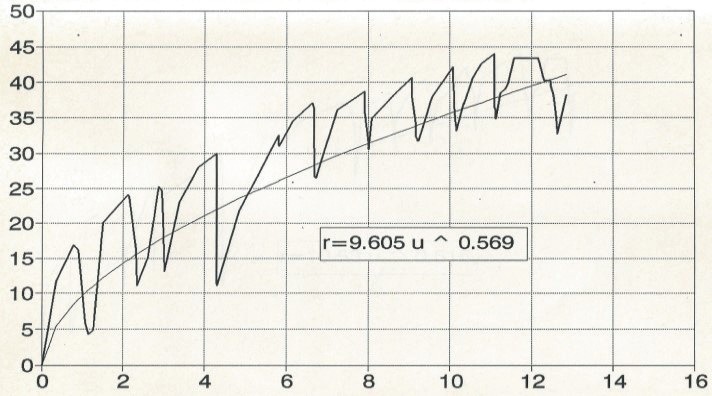
Rys. 6. Krzywa doświadczalna oporu wzdłużnego podkładu uzyskana na stanowisku nr 3 (60E1/podkłady
strunobetonowe) wraz z krzywą aproksymującą (podkład nr 1)
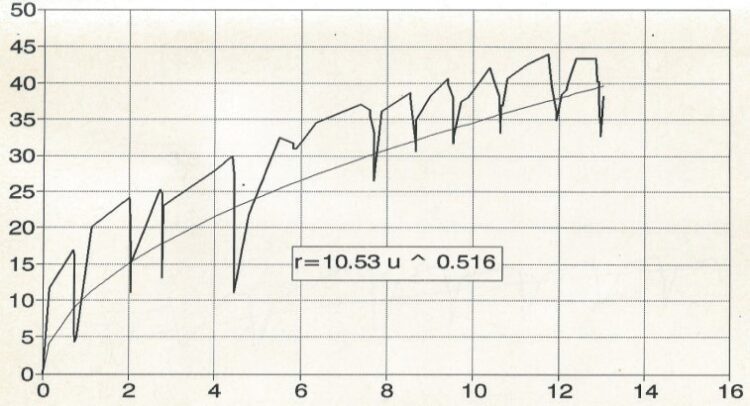
Rys. 7. Krzywa doświadczalna oporu wzdłużnego podkładu uzyskana na stanowisku nr 3 (60E1/podkłady
strunobetonowe) wraz z krzywą aproksymującą (podkład nr 2)
Na krzywych doświadczalnych pokazanych na rys. 6 i 7 można zauważyć skokowe zmiany oporu wzdłużnego, które spowodowane są rekonfiguracjami ziaren podsypki występujących skokowo po pokonaniu siły tarcia pomiędzy poszczególnymi ziarnami tłucznia. Mogą one być także efektem pewnych niejednorodności w przykładaniu siły rozpychającej przekazywanej przed podkład na tłuczeń. Takie zachowanie tłucznia świadczy o dużej roli składowej siły tarcia w całkowitym oporze wzdłużnym. Tego typu „skoki” pojawiają się także w trakcie eksploatacji toru, zwłaszcza przy wystąpieniu drgań podczas przejazdu pociągu. W praktyce są one zauważane przez służbę drogową.
Wyniki pomiarów wykonanych na torze z szynami S60 (obecnie 60E1) oraz z podkładami drewnianymi pokazano na rys. 8.
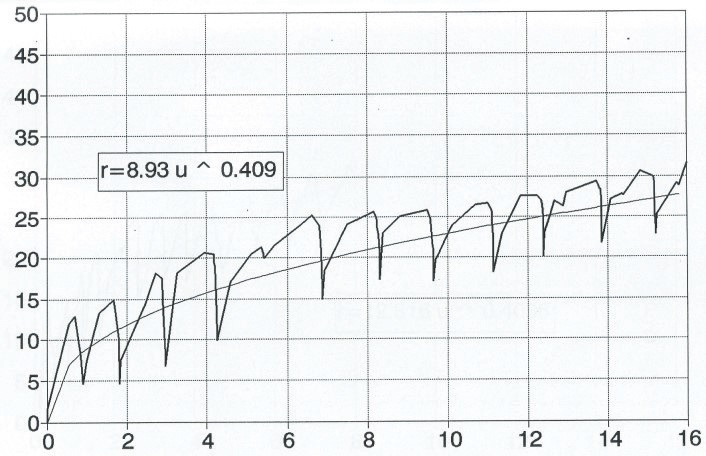
Rys. 8. Krzywa doświadczalna oporu wzdłużnego podkładu uzyskana na stanowisku nr 2 (60E1/podkłady
drewniane) wraz z krzywą aproksymującą (podkład nr 2)
>>> System pomiaru obciążeń pionowych typu SMCV
>>> Georuszty heksagonalne w stabilizacji podtorza
Model toru bezstykowego
Autorzy wprowadzili własny model toru bezstykowego na obiekcie mostowym z uwzględnieniem efektów eksploatacyjnych, takich jak: drgania podsypki wywołane ruchem kolejowym oraz pełzanie i relaksacja toru w trakcie eksploatacji. Ogólny model współpracy most–tor pokazano na rys. 9.
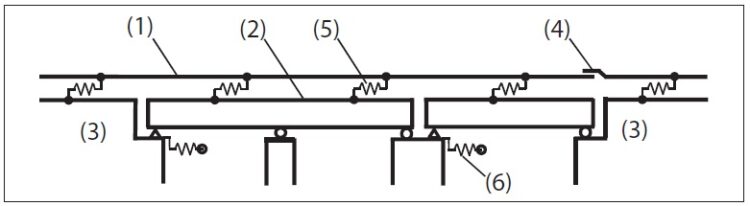
Rys. 9. Model współpracy obiektu mostowego z nawierzchnią kolejową według [1]: 1 – tor, 2 – przęsło mostu, 3 – przyczółek, 4 – przyrząd wyrównawczy (jeśli występuje), 5 – opór wzdłużny toru, 6 – model sztywności podpory obiektu
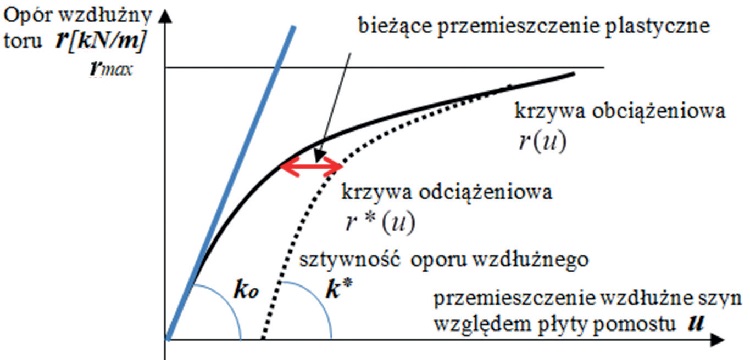
Rys. 10. Model oporu wzdłużnego toru na obiekcie mostowym uwzględniający przytwierdzenia i opór podkładów
w podsypce [9]
Model oporu wzdłużnego toru według [9] przedstawiono na rys. 10. Przyjęto następujące założenia: układ jest jednowymiarowy (rozważane są tylko przemieszczenia wzdłużne, a zmienną niezależną jest współrzędna wzdłuż toru X), szyny stanowią jedną liniowo-sprężystą belkę pryzmatyczną, opór wzdłużny jest ciągły oraz składa się z oporu wzdłużnego przytwierdzeń i podkładów. Układ równań równowagi jest następujący [10]:
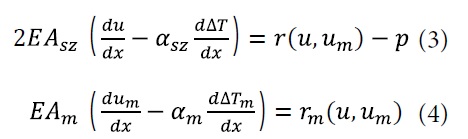
gdzie:
u – przemieszczenie wzdłużne szyny,
um– przemieszczenie wzdłużne mostu,
r – opór wzdłużny toru (podkłady wraz z przytwierdzeniami),
rm – opór wzdłużny podsypki w korycie balastowym,
p – obciążenie wzdłużne pociągiem hamującym lub przyspieszającym,
E, Asz (X) – moduł Younga oraz powierzchnia przekroju poprzecznego szyny, która może być zmienna np. w przyrządach wyrównawczych (jeśli będą zastosowane),
E, Am – moduł Younga oraz powierzchnia przekroju poprzecznego mostu,
αsz– współczynnik rozszerzalności termicznej stali szynowej,
αm– współczynnik rozszerzalności przęsła mostu,
∆Tsz – zmiana temperatury szyn,
∆Tm– zmiana temperatury mostu (temperatura efektywna).
Do przedstawionego powyżej układu równań należy jeszcze dodać warunki brzegowe oraz warunki równowagi pomiędzy oporami wzdłużnymi toru i oporem podsypki w korycie balastowym [10]. Układ ten został rozwiązany metodą różnic skończonych we własnym programie komputerowym.
Do opisu oporu wzdłużnego autorzy przyjęli następujące równanie:
r = r[u(x, t), u(x, t), t ] (5)
gdzie: u = u(X, t) przemieszczenie wzdłużne szyn (belki torowej).
Zakładając, że charakterystyka ta nie zależy jawnie od czasu oraz od prędkości przemieszczenia, tzn. u = u(X, t), wprowadza się następującą funkcję, w której k0 jest pochyleniem stycznej początkowej:
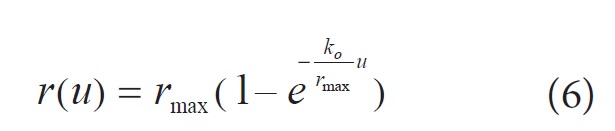
lub po przekształceniach:
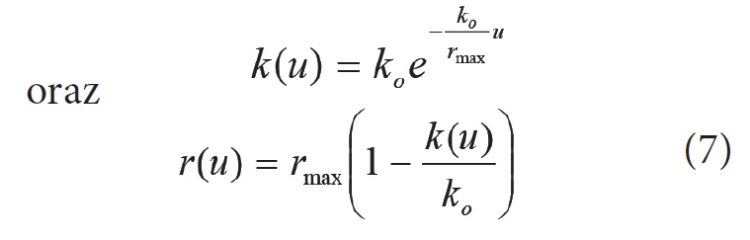
Po uwzględnieniu części plastycznej oporu wzdłużnego może on być przedstawiony jako suma części sprężystej i części plastycznej:
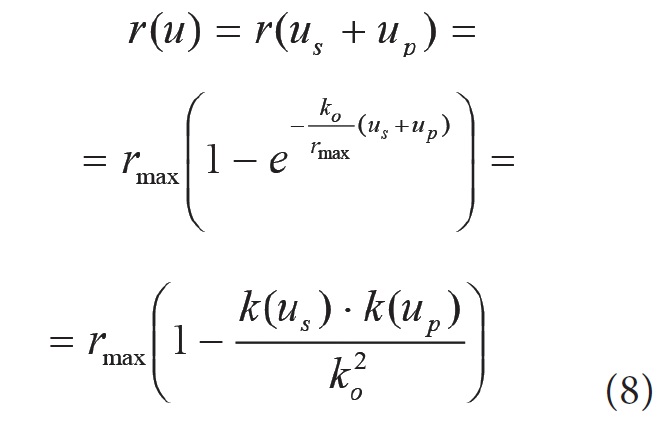
gdzie: us, up przemieszczenie sprężyste oraz przemieszczenie plastyczne.
Proces odciążania jest nieliniowy i jest modelowany z wykorzystaniem pewnego współczynnika sterującego η, dzięki któremu styczna odciążeniowa jest określona jako:
![]()
gdzie:
k0 – styczna początkowa jak przy obciążaniu,
ku – styczna bieżąca jak przy obciążaniu,
![]()
Wartość współczynnika η = 0 oznacza odciążanie liniowe (największa dyssypacja energii), natomiast gdy η = 1, wtedy odciążanie odbywa się po tej samej krzywej co obciążanie i dyssypacja wynosi 0. W przedziale [0÷1] odbywa się zatem sterowanie odciążaniem, a tym samym dyssypacją energii.
Aby określić energię dyssypowaną dla danego przemieszczenia podłużnego, należy ustalić przemieszczenie plastyczne dla bieżącego przemieszczenia całkowitego. Po przekształceniach można pokazać, że wyrażenie na przemieszczenie plastyczne ma postać:
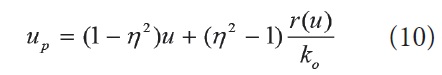
Na obiekcie mostowym powyższe przemieszczenie plastyczne będzie zmniejszało naprężenia w szynach, ponieważ w wyniku jazdy pociągów i drgań wywołanych przejazdami przemieszczenie to będzie wpływało korzystnie na redukcję naprężeń w szynach w wyniku pokonania siły tarcia w obrębie samego tłucznia skutkującego rekonfiguracją ziaren tłucznia (jak zaobserwowano podczas pomiarów oporów wzdłużnych – rys. 6 i 7) oraz w wyniku pokonania siły tarcia pomiędzy korytem balastowym a tłuczniem. Przemieszczenie powyższe (10) będzie miarą poślizgu podsypki w korycie balastowym.
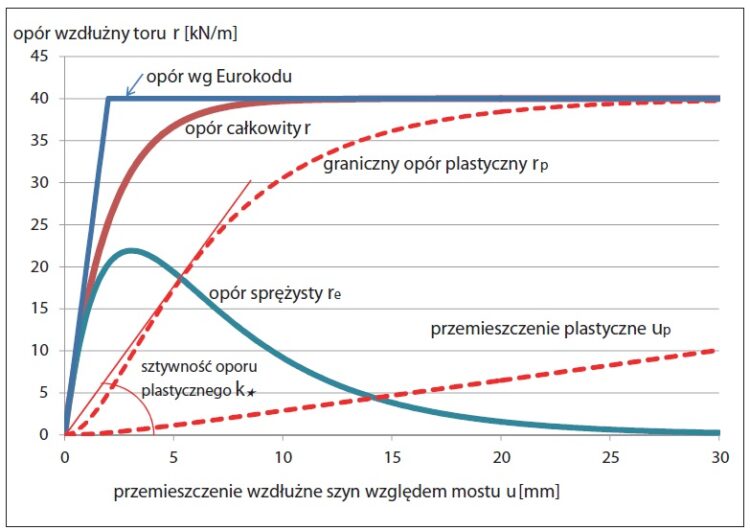
Rys. 11. Model nieliniowego oporu wzdłużnego (4) na tle oporu sprężysto-plastycznego według Eurokodu [1].
Sztywność początkowa oporu ko (4) jest taka sama, jak oporu sprężysto-plastycznego według Eurokodu, natomiast sztywność początkowa odpowiadająca oporowi plastycznemu jest określona wzorem (9). Współczynnik η = 0,80
Przykład aproksymacji oporu wzdłużnego z wykorzystaniem modelu oporu wzdłużnego (1) pokazano na rys. 11.
Na podstawie przykładowych charakterystyk oporów wzdłużnych (rys. 7) można stwierdzić, że nie występuje wyraźna granica oporu sprężystego w przypadku zastosowania funkcji (4) oraz że po przekroczeniu wartości przemieszczenia wzdłużnego ok. 2,0 mm udział oporu sprężystego w całkowitym oporze wzdłużnym znacząco maleje. Oznacza to, że powiększają się przemieszczenia plastyczne (trwałe) szyn.
Charakterystyka oporu plastycznego rp stanowi „obwiednię” minimalną oporu wzdłużnego przy jednokrotnym obciążeniu termicznym, poza którą wartość oporu wzdłużnego nie może się znaleźć. Przemieszczenie plastyczne szyn up wynosi ok. 10 mm przy całkowitym przemieszczeniu na końcu przęsła 29,3 mm (rys. 3). Oznacza to, że w trakcie przemieszczania się przęsła mostu wartość up wynika z przemieszczania się kamieni tłucznia oraz z odkształcenia warstwy podsypki pod podkładem (tutaj 35 cm).
Efekt jest taki, jak gdyby temperatura efektywna mostu była mniejsza w proporcji ok. 10 mm/29,3 mm x 36°C = 12,3°C, czyli tak jakby przyrost temperatury przęsła wynosił ok. 24°C. Przy czym należy wziąć pod uwagę, że jest to jedynie efekt powstawania przemieszczeń trwałych w podsypce, bez uwzględnienia ruchu pociągów.
Przy wyznaczaniu oporu zastępczego toru, który uwzględnia opór wzdłużny przytwierdzeń oraz podkładów w podsypce, korzystano z relacji szeregowego łączenia oporów (ściślej mówiąc, sztywności oporów). Takie ujęcie w przypadku nieliniowych charakterystyk wymaga wyznaczania sztywności zastępczej dla przyjętych kroków przemieszczenia wzdłużnego (np. co 0,1 mm). Ogólny wzór opisujący szeregowe składanie sztywności oporów jest następujący:
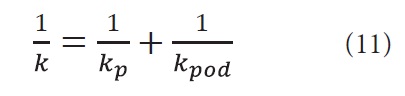
gdzie:
k – sztywność zastępcza oporu wzdłużnego toru,
kp – sztywność oporu wzdłużnego przytwierdzeń,
kpod – sztywność oporu wzdłużnego podkładów w podsypce.
Opory wzdłużne przytwierdzeń kolejowych przyjęto według badań laboratoryjnych [12]. Dla przytwierdzenia typu SB-4 przy- jęto opór wzdłużny maksymalny 18,9 kN, przemieszczenie w zakresie liniowym: 6 mm. Wartość oporu wzdłużnego przytwierdzenia typu K na podkładach drewnianych w średnim stanie technicznym przyjęto orientacyjne na 10 kN, a zakres pracy liniowej na 6 mm. Wyniki wyznaczania charakterystyk oporu wzdłużnego pokazano na rys. 12.
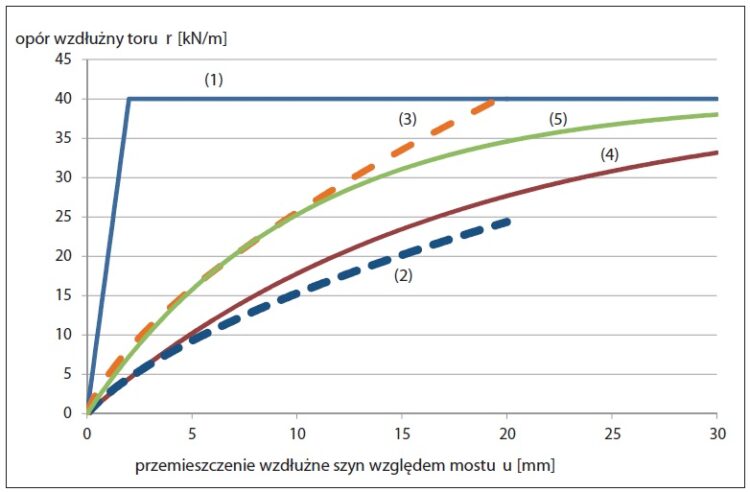
Rys. 12. Modele nieliniowego oporu wzdłużnego toru z wykorzystaniem badań: 1 – opór według Eurokodu [1],
2 – opór według badań [7] dla podkładów drewnianych z przytwierdzeniem K, 3 – opór według badań [7] dla
podkładów strunobetonowych z przytwierdzeniem SB-4 [7, 10], 4 – aproksymacja oporu z podkładami drewna
według wzoru zaproponowanego przez autorów, 5 – aproksymacja oporu z podkładami strunobetonowymi według wzoru zaproponowanego przez autorów
Tab. 3. Współczynniki równania aproksymacyjnego (8) z uwzględnieniem (10)

W II części artykułu została przedstawiona walidacja modelu toru bezstykowego na analizowanym obiekcie mostowym. Dokonana zostanie ponadto analiza obiektu, polegająca na porównaniu wartości naprężeń i przemieszczeń w odniesieniu do dwóch przypadków modelu oporu wzdłużnego podsypki: sprężysto-plastycznego (normowego) oraz wprowadzonego nieliniowego z dyssypacją energii.
Druga część artykułu dostępna jest w numerze 11/2023 miesięcznika „Inżynier Budownictwa”.

prof. dr hab. inż. Włodzimierz Czyczuła
Politechnika Krakowska,
Wydział Inżynierii Lądowej

dr hab. inż. Juliusz Sołkowski, prof. PK
Politechnika Krakowska,
Wydział Inżynierii Lądowej
Fot. i rys. archiwum autorów
Literatura
- PN-EN 1991-2:2007 Eurokod 1 – Oddziaływania na konstrukcje – Część 2: Obciążenia ruchome mostów.
- Projekt wykonawczy obiektu mostowego nad rzeką Wisłoka na linii E30, Frej Projekt, 2015.
- PN-EN 1991-1-5:2005 Eurokod 1 – Oddziaływania na konstrukcje – Część 1-5: Oddziaływania ogólne. Oddziaływania
- L. Fryba, Dynamics of Railway Bridges, Thomas Telford Publishing, Academia Praha, 1996.
- W. Czyczuła, A. Massel, K. Towpik et al., Empirical research of CWR track long term behavior for ERRI D-202/3, Kraków–Warszawa–Gdańsk 1997.
- W. Czyczuła, J. Sołkowski, K. Towpik, Interaction between CWR track and Bridges in longitudinal direction, „Archives of Civil Engineering” vol. XLIII, no. 1, 1997, s. 51–69.
- W. Czyczuła et al., Warunki budowy i utrzymania toru bezstykowego na mostach dużych rozpiętości z korytem balastowym, Prace Instytutu Inżynierii Drogowej i Kolejowej, Politechnika Krakowska, Kraków 1995.
- H. Onysyk, Analiza zmian temperatury stalowej konstrukcji mostu przez Wisłę w Puławach, „Drogi i Mosty” nr 1/2012, s. 35–52.
- J. Sołkowski, Propozycja modelu reologicznego toru bezstykowego, konferencja TRANSCOMP, Zakopane 2005, s. 36–45.
- W. Czyczuła, Tor bezstykowy, Monografia, Wydawnictwo Politechniki Krakowskiej, Kraków 2002.
- W. Czyczuła, P. Kozioł, Odpowiedź dynamiczna drogi szynowej jako struktury dwuwarstwowej w kierunku wzdłużnym, konferencja NOVKOL, Zakopane 2020.
- Ł. Chudyba, Sprężyste systemy przytwierdzeń do podkładów strunobetonowych – porównanie cech eksploatacyjnych systemów przytwierdzeń SB oraz W-14, „Przegląd Komunikacyjny”nr 11/2017, s. 27–32.