Aby kanalizacja deszczowa spełniała swoją rolę musi być zaprojektowana z wykorzystaniem współczesnych modeli opadów maksymalnych.
Kanalizacja deszczowa zgodnie z aktualnymi parabolistycznymi modelami opadów
Dotychczas stosowana formuła na natężenie deszczów, oparta na danych opadowych z przełomu XIX i XX w., zaniża obecne natężenia opadów projektowych średnio o 40% we Wrocławiu (dla danych z lat 1960-2009) [11] oraz średnio o 36% w Warszawie i o 33% na terenie całego kraju (dla danych z lat 1986-2015) [12]. Nie może być więc nadal stosowana, gdyż wymagałaby „sztucznej” korekty częstości opadów [2], [11]. W pracy [2] postuluje się, aby do czasu opracowania i upowszechnienia Polskiego Atlasu Natężeń Deszczów (PANDa) – na wzór atlasu KOSTRA (Koordinierte Starkniederschlagsregionalisierung – Auswertung) w Niemczech – stosować do metody maksymalnych natężeń (MMN) współczesne modele opadów maksymalnych. Częstości projektowe opadów powinny być już obecnie podwyższane względem standardów [4-7], np. w granicach zaproponowanych w tab. 4, ze względu na zmiany klimatu w przyszłości.
Na przykład we Wrocławiu stosować można lokalny, probabilistyczny model opadów maksymalnych GED (oparty na pomiarach z lat 1960-2009 [11]), dla zakresów: td e[5; 4320] minut i C e[1; 100] lat, o postaci IDF [2]
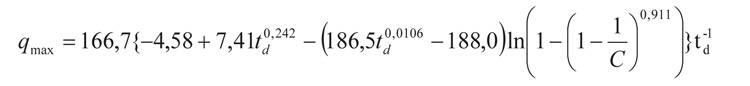
wzór nr 2
gdzie: qmax – maksymalne jednostkowe natężenie deszczu [dm3/(s-ha)]; td – czas trwania deszczu [min]; C – częstość (powtarzalność występowania) deszczu [lata].
Na terenie całego kraju można natomiast stosować regionalny, probabilistyczny model opadów maksymalnych Bogdanowicz-Stachy (oparty na pomiarach z lat 1960-1990 [13]), dla zakresów: td ∈[5; 4320] minut i C ∈[2; 100] lat, o postaci IDF [2]:
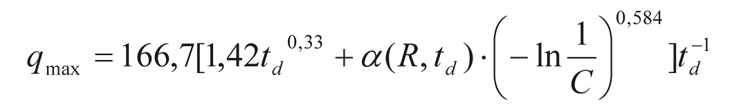
wzór nr 3
gdzie: α(R, td) – parametr (skali) zależny od regionu Polski (Ri) i czasu (td) trwania deszczu [2, 13].
Model opadów maksymalnych Bogdanowicz – Stachy (3) nie obejmuje obszarów podgórskich i górskich. Nie może być też stosowany dla częstości deszczy pojawiających się raz na rok (C = 1), wg [1,2, 11, 14].
Sprawdź też: Woda wyzwaniem w planowaniu miast

Fotolia
Kanalizacja deszczowa – dobór średnicy i spadków
Uwzględniając prognozowany wzrost intensywności opadów w przyszłości, jako minimalną średnicę kanałów deszczowych, w miastach zaleca się obecnie przyjmować Dmin = 0,40 m, a tylko w uzasadnionych przypadkach stosować można D = 0,30 m – na początkowych odcinkach sieci i przy znacznych spadkach terenu, na podstawie symulacji komputerowych dla przyszłych
obciążeń opadami wg podręcznika [2].
Kanały deszczowe należy dobierać na niecałkowite wypełnienie, tj. maksymalnie do 90% przepustowości całkowitej (Qo) danego przekroju (np. średnicy D) kanału, wg zaleceń DWA-A118 z 2006 r. [10], czyli do względnego wypełnienia: h/D < 0,75 – dla kanałów o przekroju kołowym (o średnicy D); h/H < 0,79 – dla kanałów jajowych (o wysokości przekroju H = 1,5B) oraz h/H < 0,72 – dla kanałów dzwonowych (o wysokości przekroju H = 0,85B, gdzie B oznacza szerokość przekroju w tzw. pachach).
Minimalne spadki dna kanałów deszczowych można określać ze znanej formuły: imin = 1/D (imin [‰] dla D [m]). Przykładowo dla Dmin = 0,40 m, imin = 1/0,40 = 2,5‰, przy czym dla D > 1,0 m, imin = 1,0‰. Jednakże dla małych względnych wypełnień, h/D < 0,3, powinny być one większe niż obliczane z formuły 1/D, głównie ze względu na warunki transportu zawiesin mineralnych. Z punktu widzenia hydromechaniki transport zanieczyszczeń w kanałach deszczowych można zapewnić, jeżeli opór tarcia wyrażony stycznymi naprężeniami ścinającymi będzie większy od τmin = 1,5 Pa. Wówczas wzór na imin ma postać [2]:
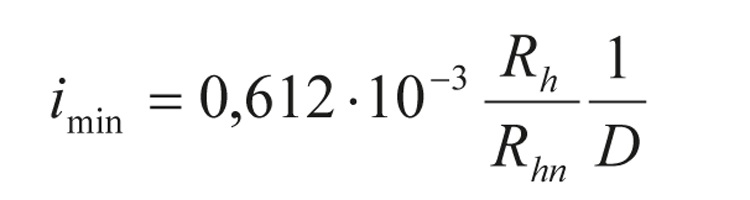
wzór nr 4
gdzie: D – średnica (wewnętrzna) kanału ściekowego [m]; Rhn – promień hydrauliczny przy częściowym wypełnieniu kanału [m]; Rh – promień hydrauliczny przy całkowitym wypełnieniu kanału (Rh = D/4) [m].
Dla przykładu: dla kanału deszczowego o średnicy Dmin = 0,40 m, z formuły 1/D spadek minimalny wynosi imin = 2,5‰
Z obliczeń wg wzoru (4) otrzymamy: dla h/D = 10% imin = 6,0‰; dla h/D = 20% imin = 3,2‰; a dla h/D = 30% imin = 2,2‰. Tak obliczone spadki dla względnych wypełnień h/D < 0,3 gwarantują samooczyszczanie się kanałów deszczowych. Są też większe od obliczonych z warunku zachowania prędkości minimalnej Vmin = 0,8 m/s – przy całkowitym wypełnieniu, gdyż wówczas dla Dmin = 0,40 m, imin= 2,3‰.
Maksymalne spadki dna kanałów deszczowych powinny wynikać z warunku nieprzekraczania prędkości Vmax = 5,0 m/s – przy całkowitym wypełnieniu kanału. Przykładowo dla Dmin = 0,40 m, imax = 90‰ . Szczegółowe zasady obliczeń podane są w podręczniku [2].
Powyższa treść jest kontynuacją pierwszej części >>>
Podsumowanie dwóch części artykułu:
Zaprezentowano ewolucje europejskich standardów projektowania systemów odwodnień terenów zurbanizowanych: PN-EN 752:2000/2001, PN-EN 752:2008 i PN-EN 752:2017, z uwzględnieniem rozporządzenia MTiGM z 1999 r. (dotyczącego odwadniania dróg), oraz dokonano ich interpretacji. Ponieważ grawitacyjne systemy kanalizacji deszczowej projektowane są zwykle na perspektywę 50-100 lat, właściwe jest uwzględnianie zagrożeń wynikających z prognozowanych zmian klimatu w horyzoncie czasowym roku 2100. Dotyczy to zwłaszcza zagrożeń wynikających ze wzrostu intensywności i częstości występowania ekstremalnych opadów w przyszłości.
Na tych podstawach do wymiarowania kanalizacji deszczowej zalecono metodę maksymalnych natężeń (MMN) jako bezpieczną metodę bilansowania strumieni wód opadowych. Do czasu opracowania i upowszechnienia Polskiego Atlasu Natężeń Deszczów (PANDa) – na wzór atlasu KOSTRA w Niemczech – należy do MMN stosować współczesne, probabilistyczne modele opadów maksymalnych (lokalne i regionalne). Trzeba też przy tym przyjmować większe częstości opadów projektowych niż zalecane w dotychczasowych standardach projektowych (PN-EN 752:2000/2001, PN-EN 752:2008 i PN-EN 752:2017 oraz MTiGM z 1999 r,), co pozwoli prawdopodobnie na zachowanie także w przyszłości obecnie dopuszczalnych częstości zagrożeń wylewami z kanałów.
Podobne zalecenia i działania podejmowane są już lokalnie w państwach europejskich (Belgia, Niemcy).
Literatura
- A. Kotowski, Wyzwania wywołane zmianami klimatu w projektowaniu systemów odwodnień terenów w Polsce, „Inżynier Budownictwa” nr 3/2013.
- A. Kotowski, Podstawy bezpiecznego wymiarowania odwodnień terenów. Sieci kanalizacyjne (t. I); Obiekty specjalne (t. II), Wyd. Seidel-Przywecki, Warszawa 2011 (wyd. I), 2015 (wyd. II).
- IPCC: Impacts, Adaptation and Vulnerabi- lity, Panel on Climate Change, Cambridge University Press, 2014.
- PN-EN 752:2000/2001 Zewnętrzne systemy kanalizacyjne.
- PN-EN 752:2008 Drain and sewer systems outside buildings.
- PN-EN 752:2017 Drain and sewer systems outside buildings – Sewer system mana- gement.
- Rozporządzenie Ministra Transportu i Gospodarki Morskiej z dnia 2 marca 1999 r. w sprawie warunków technicznych, jakim powinny odpowiadać drogi publiczne i ich usytuowanie (Dz.U. z 1999 r. Nr 43, poz. 430).
- P. Willems, Revision of urban drainage design rules based on extrapolation of design rainfall statistics, Proc. 12th Internat. Conf. on Urban Drainage, Porto Alegre, 2011.
- Merkblatt Nr 4.3/3: Bemessung von Misch- und Regenwasserkanalen. Teil 1: Klima- wandel und móglicher Anpassungsbedarf, Bayerischen Landesamtes fur Umwelt, 2009.
- DWA-A118:2006 Hydraulische Bemessung und Nachweis von Entwasserungssyste- men, DWA, Hennef 2006.
- A. Kotowski, B. Kaźmierczak, A. Dancewicz, Modelowanie opadów do wymiarowania kanalizacji, Wyd. KILiW PAN, Warszawa 2010.
- P. Licznar, K. Siekanowicz-Grochowina, M. Oktawiec, A. Kotowski, E. Burszta- -Adamiak, Empiryczna weryfikacja formuły Błaszczyka do obliczania wartości natężenia deszczu miarodajnego, „Ochrona Środowiska” nr 2/2018.
- E. Bogdanowicz, J. Stachy, Maksymalne opady deszczu w Polsce. Charakterystyki projektowe, Wyd. IMGW, seria: Hydrologia i Oceanologia nr 23, Warszawa 1998.
- P Licznar, E. Burszta-Adamiak, A. Kotowski, K. Siekanowicz-Grochowina, M. Oktawiec, Empiryczna weryfikacja modelu Bogda- nowicz-Stachy do obliczania wartości natężenia deszczu miarodajnego, „Ochrona Środowiska” nr 3/2018.
Zobacz również: Innowacyjne parki wodne pomagają w małej retencji