Szacowanie strat ciepła z instalacji przemysłowych – cz. I

Straty ciepła zawsze towarzyszą wytwarzaniu i przesyłowi energii w postaci ciepła. Są one ograniczane osłonami termicznymi, w których główną rolę odgrywa izolacja. Zwiększenie jej grubości prowadzi do zmniejszenia strat, co jednocześnie pozwala na obniżenie temperatury medium na początku instalacji. Proces obliczania strat z nowymi warunkami początkowymi powinno się prowadzić iteracyjnie, do momentu aż spełnione zostanie przyjęte kryterium zbieżności. Grubość izolacji może też wynikać z ograniczeń technicznych bądź wymagań bezpieczeństwa. Coraz częściej optymalna grubość izolacji wyznaczana jest jako ekonomicznie uzasadniona. Trudność w jej poprawnym ustaleniu wynika głównie z powodu konieczności przyjęcia wskaźników ekonomicznych, w tym prognoz zmian cen energii lub kosztów jej wytwarzania na potrzeby procesu technologicznego.

Straty ciepła w rzadkich przypadkach można określić bezpośrednio przez pomiar, częściej określa się je na etapie projektu obliczeniowo.Można też dokonać oszacowania strat przez pomiar pośredni. Wyniki zarówno pomiarów, jak i obliczeń strat związane są z parametrami transportowanego medium, osłon termicznych oraz otoczenia zewnętrznego. Często istnieje także potrzeba oszacowania strat ciepła z już istniejącej instalacji, często o złym stanie technicznym izolacji, np. celu sporządzenia audytu energetycznego. Aby tego dokonać, można się posłużyć termografią. Pomiary termowizyjne są obecnie powszechnie wykorzystywanym narzędziem diagnostycznym. Pozwalają one dokonać pomiaru rozkładu temperatury na powierzchni w celu uzyskania informacji jakościowej lub ilościowej. Aby pomiar temperatury z użyciem kamery termowizyjnej był użyteczny, musi być wykonany w warunkach minimalizujących powstanie dodatkowych błędów pomiaru temperatury.

W artykule skoncentrowano się na problematyce związanej z oszacowaniem strat ciepła różnymi metodami. Zwrócono uwagę na potrzebę uzyskania jak najdokładniejszych pomiarów temperatur, tak aby zarówno diagnoza jakościowa, jak i ilościowa, służąca oszacowaniu strat związanych z akumulowaniem lub transportem ciepła medium, którym najczęściej są gorąca woda lub para, była jak najdokładniejsza.

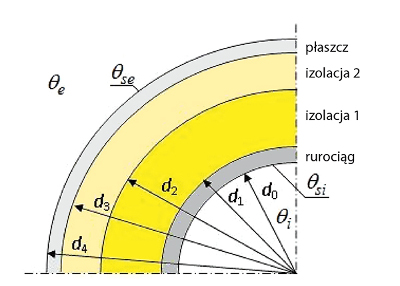
Rys. 1 Przekrój czterowarstwowego izolowanego rurociągu z warstwami o współczynniku przewodzenia ciepła λ

Obliczanie strat ciepła instalacji

Zasady obliczania strat ciepła przedstawiono m.in. w normie [1] dotyczącej izolacji cieplnej wyposażenia budynków i instalacji przemysłowych. Aby dokonać obliczeń, wymagana jest znajomość geometrii obiektów i właściwości fizycznych materiałów, z których zostały one wykonane. Straty ciepła oprócz tego, że rosną ze wzrostem różnicy temperatury płynu θ w izolowanym rurociągu (obiekcie) i otoczenia θ, w największej mierze zależą od oporu cieplnego na drodze od wysokotemperaturowego płynu do otaczającego powietrza zewnętrznego bądź gruntu.Opór cieplny R jest sumą cząstkowych wartości oporów przewodzenia kolejnych warstw R_i (ścianka rurociągu, izolacja, płaszcz) oraz oporów przejmowania ciepła na powierzchni wewnętrznej rurociągu R_si oraz zewnętrznej R_se (powierzchni osłony izolacji), a jego odwrotność określany jest jako współczynnik przenikania ciepła U, określony zależnością (1).

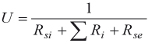
(1)

I chociaż zależność ta wygląda tak samo dla różnych geometrii, to jednak zarówno opory cieplne, jak i współczynniki przenikania ciepła w normie [1] wyrażane są w różnych jednostkach. Dla powierzchni płaskich U wyraża się w W/(m²K), dla obiektów cylindrycznych w W(m²K) oraz w W/K powierzchni dla kulistych. W podręcznikach akademickich wartość oporu cieplnego wyraża się często w K/W, uwzględniając jednak powierzchnię przegrody.

Jednostkowe straty ciepła q (w W/m² dla płaskiej przegrody oraz w W/m dla rurociągu) do otoczenia dla pojedynczego segmentu (o stałej geometrii i strukturze) można obliczyć z zależności (2).

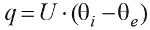
(2)

Natomiast bezwzględne straty ciepła Q, jako ilość energii traconej do otoczenia przez powierzchnię A przegrody lub na długości L odcinka rurociągu w przedziale czasu Δt, obliczyć można z zależności odpowiednio 3 albo 4.

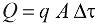
(3)

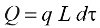
(4)

W zależności od kształtu przegrody: płaskiej, cylindrycznej czy kulistej, norma [1] określa sposób obliczania oporu cieplnego poszczególnych warstw przegrody oraz oporów przejmowania ciepła po stronie wewnętrznej i zewnętrznej przegrody. Dla „wielowarstwowego wydrążonego cylindra”, co w języku normy oznaczać może izolowany rurociąg, obliczenie oporów przewodzenia następuje z zależności (5), do której wyjaśnienia oznaczeń podano na rys. 1.

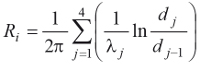
(5)

W przypadku izolowanych rurociągów wpływ oporu cieplnego samego rurociągu oraz płaszcza są często pomijalne zwłaszcza, jeśli wykonane są z metalu.

Opór przejmowania ciepła na powierzchni wewnętrznej (między transportowanym medium a ścianką rurociągu) również często się pomija ze względu na jego znikomy wpływ na wynik obliczeń, w odróżnieniu od sytuacji występującej w przegrodach budowlanych, dla których przyjmowana wartość np. poziomego przepływu ciepła R_si = 0,13 (m²K)/W jest niemal czterokrotnie większa od oporu przejmowania ciepła po stronie zewnętrznej R_se = 0,04 (m²K)/W [2]. Formalnie R_si obliczyć można z zależności (6), w której h_si to współczynnik przejmowania ciepła po stronie wewnętrznej przewodu wyrażany w W/(m²K), który w dużej mierze zależy od prędkości medium. Jego wartość waha się od 250 dla przepływu laminarnego do nawet 10 000 dla przepływu burzliwego w przypadku wody. Natomiast dla gazów i pary wodnej jego zmiany są mniejsze i wahają się od 10 do 150.

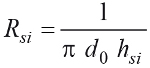
(6)

Obliczając jego wartość, np. dla rurociągu o średnicy wewnętrznej d₀ = 250 mm transportującego gorącą wodę z prędkością około 0,5–1 m/s (występujących zwykle w instalacjach), otrzymuje się R_si<0,002 (mK)/W. Wykonując analogiczne obliczenia dla pary wodnej uzyska się wartość R_si ≈ 0,01 (mK)/W. Powodem małych wartości R_si jest przede wszystkim wymuszona konwekcyjna wymiana ciepła.

Analogicznie jak R_si obliczyć można opór przejmowania ciepła dla izolowanego rurociągu po stronie zewnętrznej R_se z zależności (7)

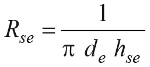
(7)

Współczynnik przejmowania ciepła h_se jest sumą dwóch składników: h_cv odpowiedzialnego za wymianę ciepła na drodze konwekcji oraz h_r uwzględniającego radiacyjną wymianę ciepła. Tutaj obliczania są bardziej złożone i uzależnione od tego, czy instalacja znajduje się wewnątrz czy na zewnątrz budynku. Stosować można empiryczne równania z normy [1]. Gdy np. rurociąg znajduje się na zewnątrz budynku, występuje najczęściej turbulentny przepływ powietrza i h_cv obliczyć można z zależności (8). Wynik jest uzależniony od prędkości wiatru ni średnicy płaszcza d_e.

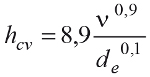
(8)

Gdy instalacja znajduje się wewnątrz budynku, zależność opisująca h_cv zależy zarówno od rodzaju opływu, różnicy temperatur płaszcza i otaczającego powietrza Δθ, jak i ułożenia instalacji. Dla instalacji ułożonej poziomo dla niewielkich średnic płaszcza (d_e<30 cm) i różnicy temperatur Δθ< 35^oC oraz poziomego ułożenia współczynnik przejmowania ciepła h_cv można opisać zależnością (9).

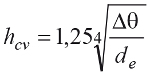
(9)

Drugi składnik odpowiedzialny jest za wymianę ciepła na drodze promieniowania. I choć jego obliczanie wydawać by się mogło proste, gdyż odbywa się z jednej zależności (10), to jednak dwa parametry – współczynnik emisyjności eoraz temperatura otoczenia T₂ – nie są łatwe do ustalenia i powodować mogą znaczne rozbieżności w wynikach.

(10)

W normie [1] wprost nie podano, o jakie temperatury chodzi w równaniu (10), lecz z prawa Stefana-Boltzmanna widomo, że chodzi o temperatury termodynamiczne (w Kelwinach) obiektów T₁ i T₂, między którymi następuje wymiana ciepła przez promieniowanie. W normie przy równaniu, którym można aproksymować równanie (10) nieco prostszą postacią, napisano, że T₂ to temperatura otoczenia lub temperatura powierzchni promieniującej w pobliżu. Stwierdzenie to wymaga komentarza, gdyż w normie nie sprecyzowano definicji temperatury otoczenia, a nie należy utożsamiać jej z temperaturą otaczającego powietrza, jak to często można znaleźć w niektórych publikacjach. Natomiast stwierdzenie, że „jest to temperatura powierzchni promieniującej w pobliżu” prawdziwe jest zazwyczaj w przestrzeniach zamkniętych. Więcej wyjaśnień na ten temat przedstawiono punkcie opisującym pomiar termowizyjny.

W obliczeniach inżynierskich [3] często przyjmuje się wartość współczynnika przejmowania ciepła h_se na zewnętrznej powierzchni izolacji równą 9 W/(m²K) dla powierzchni niemetalicznych (np. izolacji kauczukowych), 7 W/(m²K) dla płaszczy metalowych matowych, np. blachy ocynkowanej, oraz 5 W/(m²K) dla płaszczy metalowych refleksyjnych, np. aluminium lub stali nierdzewnej. Widać zmniejszanie się wartości wraz ze zmniejszaniem się współczynnika emisyjności, co wynika bezpośrednio ze zmniejszaniem wymiany ciepła przez promieniowanie.

Obliczając z zależności (8)–(10) wartość h_se np. w przestrzeni zewnętrznej rurociągu z płaszczem o temperaturze 30^oC z blachy ocynkowanej o średnicy zewnętrznej 0,8 m i przyjmując temperaturę otoczenia 0^oC oraz prędkość wiatru 0,25 m/s, otrzymuje się wartość h_se = 7 W/(m²K), czyli taką samą jak przyjmowaną do obliczeń inżynierskich. Jednak zmiana któregokolwiek z parametrów spowoduje zmianę h_se, a największy wpływ ma prędkość wiatru, co widać na wykresach pokazanych na rys. 2. Pokazano na nich jednocześnie zmianę oporu przejmowania ciepła na powierzchni zewnętrznej.

Łatwo zauważyć, że opór przejmowania ciepła po stronie zewnętrznej dla izolowanych rurociągów silnie zmienia się z prędkością wiatru i jednocześnie jest on co najmniej o rząd większy od oporu przejmowania ciepła po stronie wewnętrznej rurociągu. Czy jednak obie wartości oporów mają istotne znaczenie do obliczeniowego wyznaczanie strat ciepła? Przykładowo opór przewodzenia ciepła izolacji z wełny mineralnej, o grubości 20 cm na rurociągu stalowym o średnicy d₀ = 40 cm, wynosi 8 (m²K)/W. Wniosek: opory przejmowania ciepła w tym przypadku wynoszą około 0,6% całkowitych oporów i taki też mają udział w stratach ciepła. Czytelnik mógłby zapytać, czy w takim razie w ogóle istotne są podane zależności i związki opisujące wymianę ciepła? Gdyby jednak ten sam rurociąg był pozbawiony izolacji, to udział oporu przenikania stanowi ponad 95% całkowitych oporów cieplnych. W pewnych sytuacjach można zatem je pominąć, lecz w innych jest to niedopuszczalne. Opory przejmowania ciepła są podstawą oszacowania strat ciepła m.in. z użyciem kamery termowizyjnej, stąd też należy znać sposób ich obliczania.

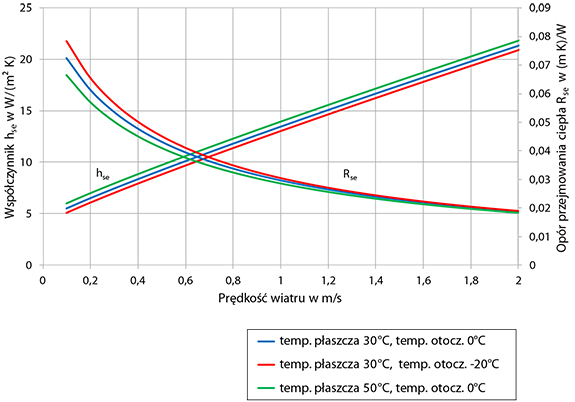
Rys. 2 Zmiana współczynnika przenikania ciepła oraz oporu cieplnego na powierzchni zewnętrznej zależnie od temperatur i prędkości wiatru

Bezpośredni pomiar strat ciepła

W przypadku transportu ciepła rurociągami straty ciepła można zmierzyć bezpośrednio. Metoda ta jest prosta, co nie oznacza, że tania w realizacji.  Wymagany jest pomiar trzech parametrów: strumienia medium oraz jego temperatury na początku i końcu rurociągu oraz obliczenie ilości energii, w analogiczny sposób jak to się realizuje, dokonując pomiaru ilości energii dostarczanej do budynków przy użyciu ciepłomierzy, korzystając z zależności (11). Czujniki temperatury, zwykle termometryczne typu Pt100, Pt500 lub Pt1000, są indywidualnie parowane przez producenta ciepłomierza, tak aby uzyskać jak najmniejsze błędy pomiaru różnicy temperatur.

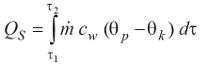
(11)

w której: Q_s – straty ciepła [J];
?– strumień masy medium [kg/s];
c_w – ciepło właściwe wody [J/(kgK)];
θ_p– temperatura medium na początku rurociągu [°C]; θ_k– temperatura medium na końcu rurociągu [°C].

Spadek temperatury w pojedynczym odcinku rurociągu transportowego często wynosi zaledwie kilka stopni, podczas gdy różnica temperatur między temperaturą zasilania i powrotu medium dostarczającym ciepło do budynku jest kilkunastokrotnie wyższa. W normie [4], dotyczącej ciepłomierzy, dla klasy 3 określono dopuszczalny błąd pomiaru temperatury jako maksymalnie wynoszący 1,5%, dla minimalnej różnicy temperatur wynoszącej Δθ_min= 3°C. Względny błąd graniczny przelicznika ETD, (wyrażony w procentach), obliczyć można w zależności od różnicy temperatury Δθ, z zależności (12):

(12)

A zatem dla mediów typu gorąca woda można liczyć na względnie mały udział w całkowitej niepewności pomiaru ciepła składnika związanego z pomiarem różnicy temperatur. Problem bardziej się komplikuje podczas pomiaru strumienia pary przegrzanej, o temperaturze ponad 500^oC. Sparowane czujniki dla takich temperatur trudno jest skompletować. Użycie standardowych czujników Pt nawet klasy A jest nieodpowiednie, gdyż niepewność pomiaru temperatury wynosi wówczas od około 1,2^oC, co przenieść się może na ponad 30% niepewność pomiaru różnicy temperatur.

Do pomiaru strumienia medium najkorzystniej jest użyć istniejący układ pomiarowy, a gdy go nie ma, można zastosować np. przepływomierz ultra­dźwiękowy z nakładanymi głowicami. Niepewność pomiaru strumienia wynosi w najlepszym przypadku 3–5% wartości mierzonej, gdy zachowane są rygory związane z warunkami pomiaru. Uwzględniając niepewność obliczania ciepła elektronicznego przelicznika ciepłomierza metodą pomiarową, uzyskać można niepewność pomiaru strat ciepła rzędu 4–10%.

dr hab. inż. Sławomir Zator

Wydział Inżynierii Produkcji i Logistyki Politechniki Opolskiej

Marta Zator

studentka Wydziału Architektury Politechniki Wrocławskiej

Bibliografia

1. PN-EN ISO 12241:2010 Izolacja cieplna wyposażenia budynków i instalacji przemysłowych – Zasady obliczania.

2. PN-EN ISO 6946:2008 Komponenty budowlane i elementy budynku. Opór cieplny i współczynnik przenikania ciepła. Metoda obliczania.

3. K. Żarski, Węzły cieplne. Poradnik projektowania, Danfoss HVAC PROJECT, 2014 (http://heating.danfoss.com/external/flash/PL/PL_project_handbook.pdf).

4. PN-EN 1434-4:2009 Ciepłomierze – Część 5: Wykonywane badania przetworników przepływu. Badania do zatwierdzenia typu.