Projektowanie obudów segmentowych tuneli drążonych tarczą – analiza przypadku

W Polsce w ostatnich latach obserwuje się dynamiczny rozwój infrastruktury drogowej wspierany zarówno przez fundusze krajowe, jak i unijne. Rozbudowa sieci drogowej wiąże się także z koniecznością budowy obiektów inżynierskich takich jak wiadukty, mosty czy tunele. W niniejszym artykule omówiony zostanie jeden z obiektów będących obecnie w trakcie realizacji – tunel T-1 pod górą Luboń Mały w ciągu trasy S19 na odcinku pomiędzy Rzeszowem a Babicą. Droga ekspresowa S19 jest częścią korytarza komunikacyjnego Via Carpatia, stanowiącego jeden z kluczowych projektów infrastrukturalnych w Polsce, mającego na celu skomunikowanie północy z południem kraju, a także włączenie Polski w szerszy system transportowy łączący Litwę, Polskę, Słowację i Węgry, a docelowo także południe Europy.

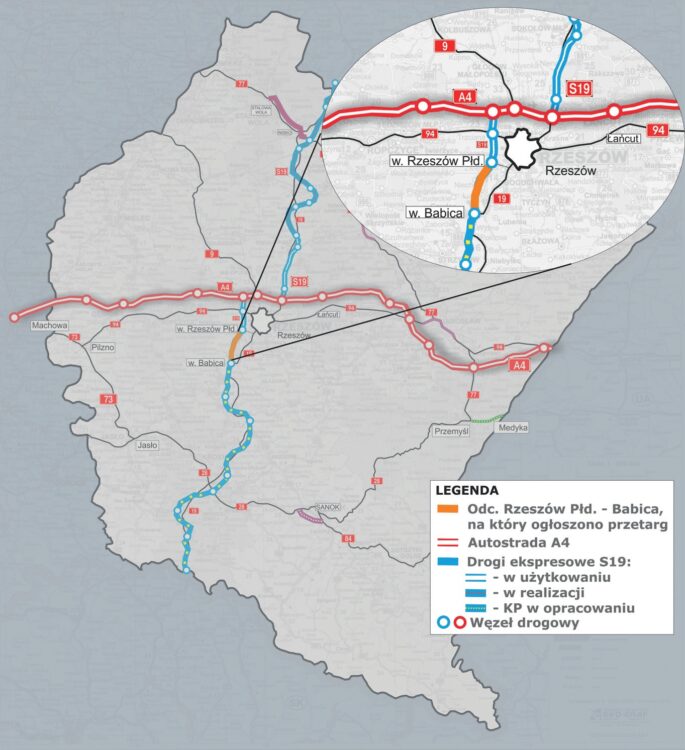
Rys. 1. Lokalizacja inwestycji na mapie Polski. Rys. 1. GDDKiA

Podstawowe założenia

Budowa tuneli na S19 jest jednym z najbardziej wymagających i innowacyjnych elementów tego przedsięwzięcia. Planowane są cztery tunele dwunawowe: T-1, T-2 (na odcinku Miejsce Piastowe–Dukla), T-3 (Babica–Domaradz) i T-4 (Dukla–Barwinek). Na rys. 1 przedstawiono lokalizację inwestycji – odcinka Rzeszów Południe–Babica na mapie województwa podkarpackiego, a na rys. 2 – szczegółową lokalizację omawianego w artykule tunelu T-1. Na wstępnych etapach projektu tunelu T-1 analizowano możliwość zastosowania różnych technologii budowy – rozważano tunel drążony zarówno metodą konwencjonalną, jak i przy użyciu tarczy zmechanizowanej (TBM – tunel boring machine). Metoda drążenia tunelu ma ogromny wpływ na jego przekrój poprzeczny. Na rys. 3 i 4 przedstawiono przekroje poprzeczne obiektu T-1 w zależności od wybranej metody budowy (rys. 3 – metoda konwencjonalna, rys. 4 – metoda tarczowa).

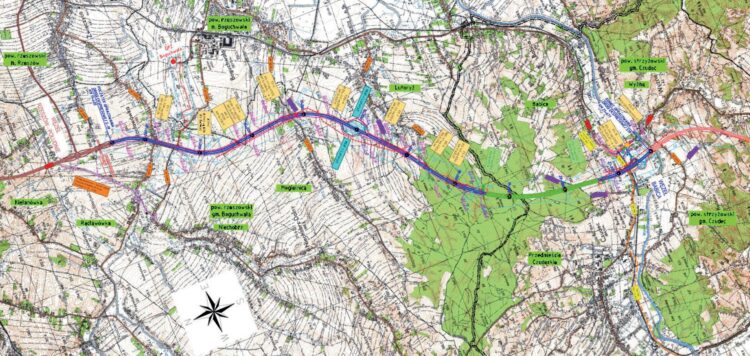
Rys. 2. Lokalizacja tunelu T-1 (w kolorze zielonym). Rys. 2. GDDKiA

Przetarg prowadzony w formule „projektuj i buduj” zawierał szczegółowe wymagania dotyczące tunelu, ale nie precyzował metody jego drążenia. Wymagania zawarte w specyfikacji przetargowej określały m.in. następujące warunki:

• przekrój tunelu dwunawowy – cztery pasy ruchu o szerokości 3,5 m, po dwa prowadzące w każdym kierunku, przy czym pasy poszczególnych kierunków ruchu umieszczone w oddzielnych nawach tunelu;
• wyposażenie tunelu w przejścia poprzeczne między nawami tunelu, rozmieszczone w odległościach nieprzekraczających 150 m, oraz przejazd awaryjny dla służb ratowniczych w połowie długości tunelu;
• wyposażenie w inne systemy bezpieczeństwa takie jak: sygnalizacja pożaru, łączności alarmowej, monitoringu i zarządzania tunelem oraz system wentylacji i oświetlenia;
• a także przyjęcie do projektu założenia, że do tunelu dopuszczony jest całodobowy wjazd pojazdów transportujących materiały niebezpieczne (kategoriaADR tunelu A), mogących wywołać pożar o mocy 100 MW.

>>> Rozpoznanie warunków geotechnicznych i wykonanie dokumentacji

>>> Badania dynamiczne w aspekcie optymalizacji fundamentów palowych

>>> Ocena obliczeń MES na podstawie monitoringu przemieszczeń

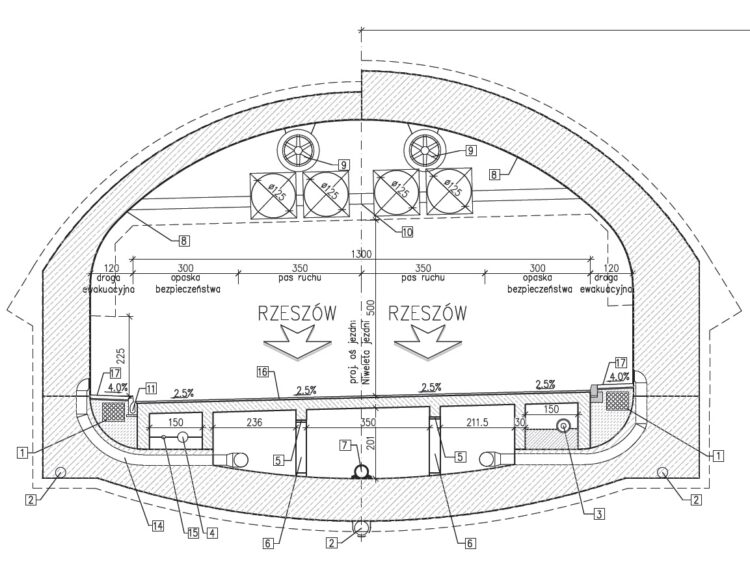
Rys. 3. Przekrój poprzeczny tunelu T-1 przy zastosowaniu metody konwencjonalnej [2]

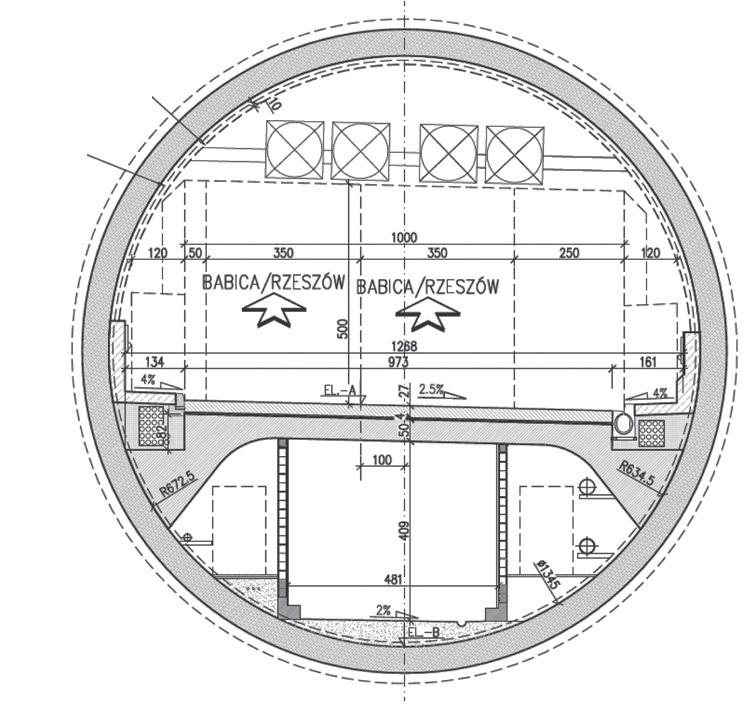
Rys. 4. Przekrój poprzeczny tunelu T-1 przy zastosowaniu metody tarczowej [7]

Wyboru metody budowy dokonano na podstawie przeprowadzonych analiz związanych z ekonomicznością danego rozwiązania, z uwzględnieniem szczegółowej analizy warunków geologicznych i geotechnicznych oraz wszelkich kryteriów określonych w warunkach przetargowych. Ze względu na długość tunelu oraz jego średnicę zdecydowano o zastosowaniu metody tarczowej (fot. 1 i 2). Wskaźniki jej wydajności są nieosiągalne w przypadku metod tradycyjnych. Technologia ta pozwala na drążenie tuneli o średnicach do 16 m z wydajnością do 20 m/dobę. Dodatkowo umożliwia osiągnięcie bardzo wysokich parametrów wodoszczelności i ognioodporności. Takie rezultaty wynikają również z ciągłego doskonalenia jednego z kluczowych aspektów technologicznych metody tarczowej – projektowania, produkcji i montażu obudowy segmentowej.

Fot. 1. Głowica tarczy zmechanizowanej przygotowana do drążenia tunelu T-1. Fot. 1. Emilia Roguska

Budowa geologiczna

Pod względem geologicznym tunel T-1 znajduje się w obszarze Karpat Zewnętrznych, który charakteryzuje się fałdowo-płaszczowinową strukturą tektoniczną. Tworzące go osady fliszowe powstały w wyniku podwodnego osadzania materiału z prądów zawiesinowych o różnej gęstości, ruchów masowych, a także sedymentacji osadów pelagicznych. Zespół utworów fliszowych składa się z naprzemianległych warstw zlepieńców, piaskowców, mułowców, margli i łupków, które formowały się w kilku basenach sedymentacyjnych przez ok. 140 mln lat, od późnej jury do wczesnego miocenu. W wyniku orogenezy alpejskiej (oligocen–miocen) osady te uległy deformacji, sfałdowaniu i oddzieleniu od podłoża, tworząc płaszczowiny – jednostki tektoniczne nasunięte od południa. W obrębie tunelu utwory fliszowe są reprezentowane przez warstwy inoceramowe, które charakteryzują się typową dla fliszu karpackiego zmiennością zarówno w profilu pionowym, jak i poziomym. Tworzą one skomplikowany układ tektoniczny z licznymi uskokami i spękaniami. Kąt upadu warstw jest zróżnicowany i waha się od 10–20° do 60–70°, co wskazuje na zaawansowany układ fałdowy.

Fot. 2. Widok tarczy zmechanizowanej przygotowanej do rozpoczęcia drążenia tunelu T-1. Fot. 2. GDDKiA

Warunki hydrogeologiczne fliszu są także skomplikowane, trudne do precyzyjnego określenia ze względu na dużą przepuszczalność i zmienność (uskoki) ośrodka. Tunel przecina obszar, w którym zostało stwierdzone występowanie lokalnego zbiornika wód podziemnych o charakterze szczelinowo-porowym, o dużych jak na warunki fliszu karpackiego zasobach [7].

>>> Kategorie i opinie geotechniczne oraz warunki geotechniczne posadowienia obiektów – przepisy

>>> Budowa drogi ekspresowej S2 pod tunelem metra w Warszawie

>>> Tunel drogowy w ciągu drogi ekspresowej S2 na odcinku Południowej Obwodnicy Warszawy

Obudowa segmentowa – charakterystyka ogólna

Istnieją różne systemy pierścieni segmentowych tuneli: pierścienie równoległe, równoległe z korekcyjnymi, pierścieni uniwersalnych (rys. 5). Układ pierścieni powinien umożliwić zarówno osiągnięcie łuków pionowych i poziomych zależnych od niwelety trasy, jak i korekcję przebiegu tunelu w przypadku jego odchylenia. Zgodnie z wytycznymi promień krzywizny korekcyjnej musi być co najmniej o 20% mniejszy niż najmniejszy projektowany promień krzywizny [4].

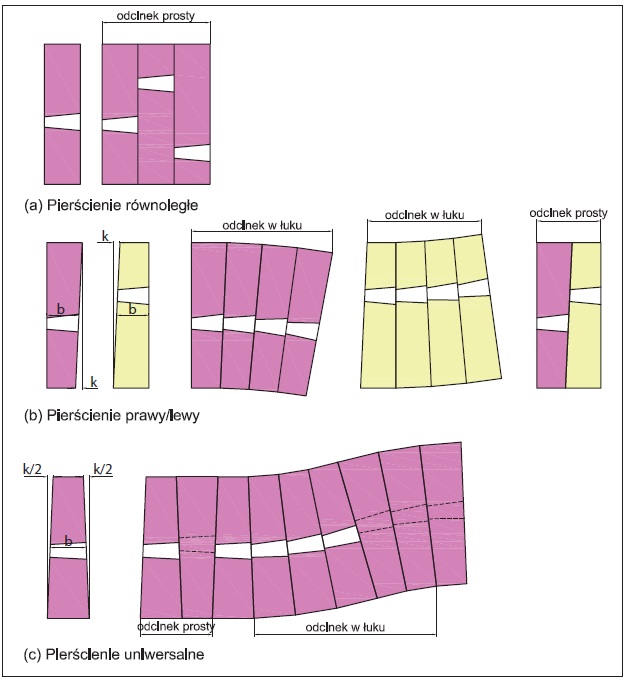
Rys. 5. Układy pierścieni obudowy segmentowej [5]

Układy pierścieni równoległych składają się z elementów o powierzchniach czołowych równoległych do siebie i prostopadłych do osi tunelu (rys. 5a). Systemy te z natury nie nadają się do krzywizn i stwarzają problemy przy uszczelnianiu. Między pierścieniami konieczne jest przywrócenie linii i nachylenia, co prowadzi do spadków siły w części uszczelek. Może to uniemożliwić utrzymanie odpowiedniej szczelności obudowy. Rozwiązaniem może być stosowanie pierścieni korekcyjnych, co jednak wymaga użycia różnych zestawów szalunków, tracona jest tym samym największa zaleta tego systemu.

Układ pierścieni prawy/lewy (rys. 5b) składa się zazwyczaj ze stożkowych pierścieni, których jedna powierzchnia obwodowa jest prostopadła do osi tunelu, a druga – nachylona. Sekwencja naprzemiennych pierścieni stożkowych prawo- i lewostronnych tworzy układ prosty. Alternatywnie, sekwencja pierścieni prawostronnie lub lewostronnie zbieżnych daje krzywą o minimalnym promieniu krzywizny. Korekcję kierunku w górę i w dół uzyskuje się poprzez obrót stożkowego pierścienia segmentowego o 90° [6]. Ten system zapewnia dobrą szczelność, ale jego wadą jest konieczność wykorzystywania różnych zestawów szalunków.

Najczęściej stosowanym układem jest obecnie układ pierścieni uniwersalnych, w którym obydwie powierzchnie obwodowe pierścienia są nachylone do osi tunelu. Jak pokazano na rys. 5c, zbieżność pierścienia jest podzielona pomiędzy dwie powierzchnie obwodowe, a wszystkie krzywe i korekty kierunku można uzyskać poprzez obrót pierścienia segmentowego. Główną zaletą tego systemu jest to, że wymagany jest tylko jeden rodzaj szalunku [4]. Stosując pierścienie uniwersalne, można uzyskać proste ustawienie, obracając każdy naprzemienny pierścień o 180°. Krzywe poziome i pionowe pokonuje się poprzez częściowy obrót pierścieni.

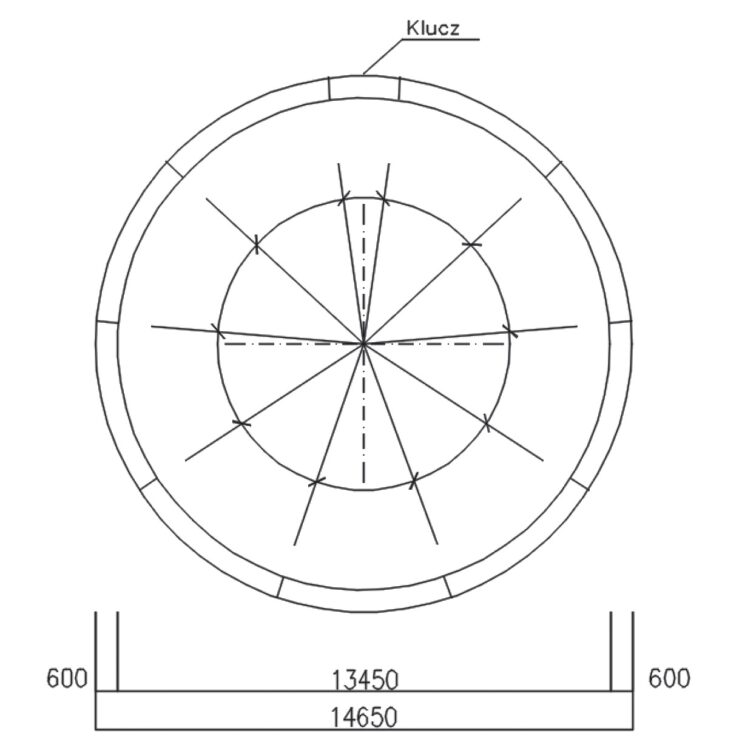
Rys. 6. Schemat obudowy segmentowej tunelu T-1. Rys. 6. autorek

Obudowa tunelu T-1 została zaprojektowana jako obudowa z pierścieni uniwersalnych o grubości 60 cm. Każdy jej pierścień składa się z dziewięciu segmentów standardowych oraz klucza. Długość pierścienia wzdłuż osi tunelu wynosi 2 m, a kąt pochylenia jego ścianek wynikający z zastosowania układu uniwersalnego – ok. 0,4°. Schemat obudowy segmentowej zastosowanej w tunelu T-1 przedstawiono na rys. 6.

Kombinacje obciążeń do projektowania obudowy segmentowej

Projekt obudowy segmentowej powinien uwzględniać nie tylko obciążenia, jakim poddawane będą segmenty od momentu produkcji przez cały okres użytkowania tunelu, ale także wszystkie wymagania technologiczne związane z procesem drążenia tunelu. Przykładowo, oprócz spełnienia wymagań konstrukcyjnych grubość segmentu powinna być wystarczająca, aby zapewnić odpowiednią przestrzeń i swobodny odstęp dla uszczelek oraz wgłębień na uszczelnienia. Należy także przewidzieć odpowiednią przestrzeń dla łożysk siłowników hydraulicznych zapewniających posuw tarczy. Wymaga to zatem dokładnej znajomości parametrów maszyny. Projektowanie obudowy jest procesem iteracyjnym, w którym konieczne jest równoczesne uwzględnienie specyfikacji maszyny drążącej i wymagań konstrukcyjnych segmentów tunelu.

Wymagania konstrukcyjne dotyczą uwzględnienia obciążeń tymczasowych wynikających z procesu produkcji i składowania elementu, stanów związanych z drążeniem tunelu i posuwem tarczy, stanu docelowego, w tym przede wszystkim obciążenia elementu parciem gruntu oraz wody gruntowej, a także stanów pożarowych.

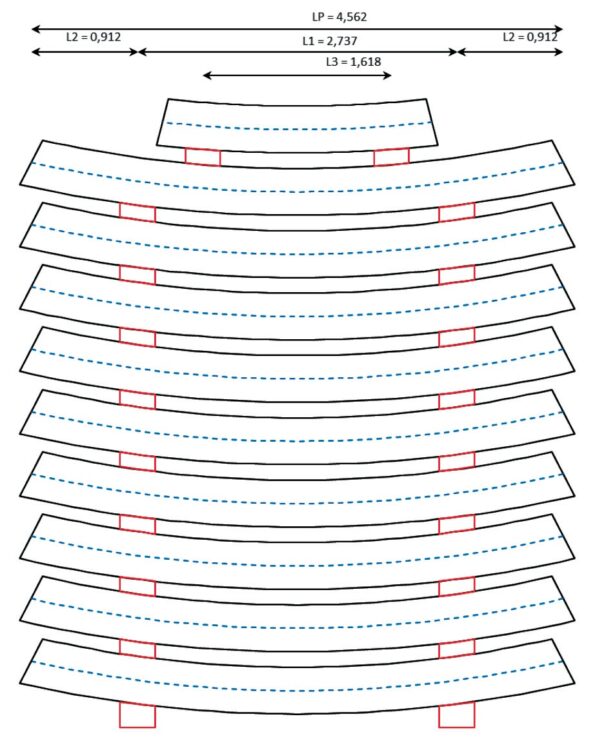
Rys. 7. Schemat składowania segmentów. Rys. GDDKiA

Obciążenia tymczasowe

Obciążenie przy rozformowywaniu odpowiada sytuacji, gdy segment jest podnoszony z formy za pomocą podnośnika podciśnieniowego. Stan ten jest analizowany jako nawis części segmentu, który znajduje się poza płytą podciśnieniową. Ze względu na wiek betonu w fazie przejściowej charakterystyczna wytrzymałość betonu na ściskanie wynosi 15 MPa. W przypadku analiz prowadzonych na S19 wpływ tego stanu obliczeniowego był pomijalny.

Fot. 3. Budowa tunelu T-1, Luboń Mały. Fot. GDDKiA

Obciążenie podczas składowania elementów (rys. 7 i fot. 3) – zakłada się, że cały pierścień będzie składowany w stosie. Analizując obciążenia w tej fazie, trzeba koniecznie uwzględnić przypadkową mimośrodowość podkładek ze względu na możliwe odchylenia w czasie ich układania. W kombinacjach obciążeniowych uwzględniono mimośrodowość każdego z rzędów podkładek jako osobny przypadek obliczeniowy.

Obciążenia pochodzące od transportu elementów obliczane są bardzo podobnie jak w przypadku składowania, gdyż elementy te transportowane są w stosach. Stosy transportowe są jednak niższe, ale obciążenia mają charakter dynamiczny, dlatego w tym przypadku w obliczeniach stosuje się współczynnik dynamiczny.

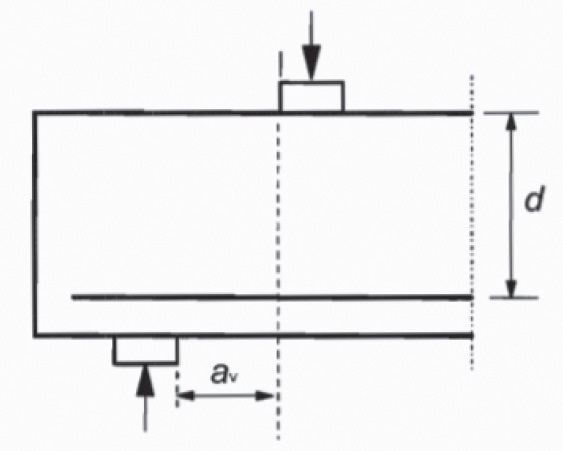
Rys. 8. Odległości a_v oraz d do obliczenia zredukowanej siły ścinającej według PN-EN 1992-1-1 [3]

Wyniki obliczeń stanów związanych ze składowaniem oraz transportem elementów prowadzą w wielu przypadkach do uzyskania wysokiej wartości siły ścinającej – w wypadku pierścieni tunelu S19 nawet wyższej niż siła uzyskiwana w stanie docelowym. Według rozdziału 6.2.2 (6) PN-EN 1992-1-1 [3] maksymalna siła ścinająca uzyskana z obliczeń może być jednak zredukowana ze względu na przyłożenie obciążenia do górnej części elementu w odległości 0 ≤ a_v ≤ 2d od krawędzi podpory (rys. 8). Udział tego obciążenia w sile poprzecznej V_Ed można pomnożyć przez β = a_v/2d. To zmniejszenie siły poprzecznej stosuje się przy sprawdzaniu przekroju na ścinanie (V_Rd,c) w przypadkach, gdy zbrojenie podłużne jest w pełni zakotwione na podporze. Jeżeli wartość a_v ≤ 0,5d, wówczas należy przyjąć a_v = 0,5d (parametry a_v oraz d przedstawiono na rys. 8).

Mimośrodowość obciążenia rozpatrywana w tym przypadku wynosi 0,15 m, więc jest mniejsza niż 0,5d, dlatego a_v może być przyjmowane jako 0,5d = 0,5(0,53) = 0,26 oraz współczynnik redukcyjny β = a_v/2d = 0,5d/2d = 0,25. Siła ścinająca może zatem zostać zmniejszona do 25% siły teoretycznej.

>>> Wentylacja w tunelach drogowych a bezpieczeństwo

>>> Zasilanie energią elektryczną tuneli

Obciążenia od siłowników zapewniających posuw tarczy

W celu zaprojektowania obudowy segmentowej z uwzględnieniem sił oddziaływania na pierścień siłowników zapewniających posuw tarczy konieczna jest znajomość wartości tych sił. Są one ograniczone od dołu przez konieczność zachowania stateczności przodka oraz od góry przez graniczne ciśnienie zapobiegające zniszczeniu gruntu nadkładu oraz zapobiegające zjawisku tzw. blow-out. Siły posuwu zależą zatem od parametrów geotechnicznych masywu gruntowego oraz od wysokości nadkładu, i w poszczególnych przekrojach mogą się od siebie znacznie różnić. Między innymi z tego powodu w projekcie założone zostały dwa rodzaje pierścieni: tzw. pierścienie lekkie oraz ciężkie. Pierścienie ciężkie są przystosowane do przeniesienia największych sił posuwu, ale mają także zastosowanie w strefach portalowych oraz miejscach, w których wykonane będą przewiązki, gdyż ich zbrojenie umożliwia otwarcie przekroju.

Model geotechniczny – stan docelowy pracy obudowy

Kluczowym elementem analizy obudowy segmentowej jest modelowanie geotechniczne, które ma na celu oszacowanie sił działających na obudowę w fazie docelowej pracy konstrukcji. W tej fazie konstrukcja jest obciążona parciem otaczającego ją masywu gruntowego (lub skalnego) oraz wody. Wartości tego obciążenia stanowią osobne kombinacje obciążeń.

W przypadku złożonych warunków geologicznych i geotechnicznych w rejonie budowy tunelu T-1 konieczne było zachowanie niezwykłej ostrożności w projektowaniu. Analizy prowadzone były z zastosowaniem metody elementów skończonych w przestrzeni 2D oraz 3D (rys. 9).

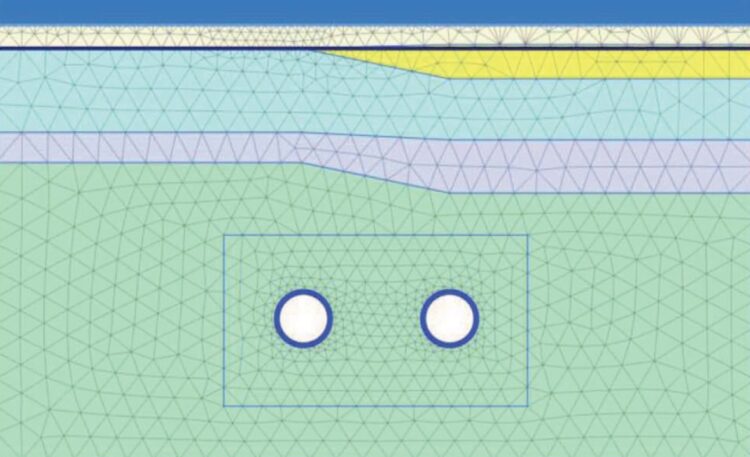
Rys. 9. Siatka elementów skończonych modelu w przestrzeni 2D [7].

Dla masywu o niewielkiej wytrzymałości na jednoosiowe ściskanie w projekcie przyjęto model Hardening Soil, który w porównaniu z modelem Coulomba-Mohra ma wiele zalet, takich jak ujęcie widocznej w testach trójosiowego ściskania hiperbolicznej zależności naprężenie–odkształcenie oraz liniowej zależności pomiędzy odciążeniem a powtórnym obciążeniem, która wynika z różnych wartości modułów. Dla warstw o wyższej wytrzymałości na jednoosiowe ściskanie przyjęto model Hoeka-Browna, który bazuje na takich parametrach jak: wartość GSI, wytrzymałość na jednoosiowe ściskanie nienaruszonej próbki skalnej oraz stałej modelu, zależnej od rodzaju skały. Parametry warstw masywu w modelu przyjęto na podstawie dokumentacji geologiczno-inżynierskiej (DGI) [2].

Modelowanie obudowy segmentowej
Ze względu na występowanie połączeń pomiędzy segmentami przyjęcie do obliczeń pełnego pierścienia o grubości równej nominalnej prowadziłoby do przeszacowania jego sztywności. W celu uwzględnienia tego faktu w projektowaniu stosuje się wzór Muir Wooda [8]:

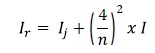gdzie:
I_j – moment bezwładności przekroju w miejscu połączenia,
I – moment bezwładności pełnego przekroju,
M – liczba segmentów tworzących pierścień (bez segmentu K „klucza”).

W miejscach połączeń między segmentami w ramach jednego pierścienia grubość segmentu została zredukowana z 60 do 48 cm, stąd:

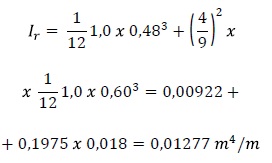
co daje redukcję sztywności giętnej przekroju prawie o 30%.

Znanych jest kilka podejść obliczeniowych do modelowania współpracy segmentowej obudowy tunelu z masywem gruntowym. Najczęściej stosowaną, ze względu na jasność założeń oraz istniejący szeroki zbiór danych literaturowych [1], jest metoda bazująca na określeniu wartości straty objętości – volume loss.

Przyjęcie straty objętości wynoszącej 1% w modelu numerycznym 2D umożliwiło uzyskanie sił wewnętrznych w obudowie, które w kolejnym kroku zostały uwzględnione przy projektowaniu konstrukcji poszczególnych elementów pierścienia. Podejście takie jest bardziej konserwatywne niż analizy trójwymiarowe, gdyż narzucona jest z góry wartość straty objętości. Dokładne jej  wyprowadzenie w modelach przestrzennych prowadzi do otrzymania mniejszych sił w obudowie, wartości te jednak są porównywalne, a analizy dwuwymiarowe są mniej czasochłonne i dają dużo więcej możliwości kalibracji. Przyjmuje się zatem, że korzystne jest prowadzenie analiz 2D, szczególnie w przypadku obiektów liniowych, gdzie nie występują nagłe zmiany warunków brzegowych ani znaczne koncentracje naprężeń. W omawianym projekcie analizy 3D wykonywane były jedynie w miejscach połączeń naw tunelu z łącznikami i przejazdami awaryjnymi.

Podsumowanie
Wykorzystanie tarcz zmechanizowanych do budowy tuneli stanowi nowoczesną i efektywną metodę drążenia tuneli w różnych warunkach geologicznych, umożliwia realizację złożonych obiektów inżynierskich, zapewniając wysoki poziom bezpieczeństwa realizacji przy jednoczesnym ograniczeniu negatywnych efektów dla otoczenia. Technologia TBM powinna być jednak postrzegana jako ciągły proces przemysłowy, a produkcja prefabrykowanych segmentów obudowy tuneli wykonywanych w tej technologii jest jego bardzo istotnym elementem. Wymaga ona szczegółowego procesu projektowania, uwzględniającego cały cykl życia produktu/segmentu obudowy: od produkcji, przez instalację, aż po eksploatację. Proces projektowania obejmuje zatem szeroki zakres scenariuszy i warunków brzegowych. W artykule omówiono jedynie wybrane, najważniejsze zasady projektowania obudowy segmentowej tuneli wykonywanych tarczami zmechanizowanymi na przykładzie projektu tunelu T-1 w ciągu trasy S19.

dr hab. inż. Monika Mitew-Czajewska, prof. PW, Politechnika Warszawska

mgr inż. Emilia Roguska, Politechnika Warszawska

Literatura
1. G. Anagnostou, K. Kovári, The Face Stability of Slurry-Shield-Driven Tunnels, „Tunnelling and Underground Space Technology”, vol. 9, no. 2, 1994, s. 165–74.
2. Dokumentacja przetargowa dla zamówienia „Zaprojektowanie i budowa drogi ekspresowej S19 na odcinku od węzła Rzeszów Południe (bez węzła) do węzła Babica (z węzłem)”.
3. PN-EN 1992-1-1 Eurocode 2: Design of Concrete Structures – Part 1-1: General Ruels and Rules for Buildings.
4. Guideline „Concrete Segmental Lining Systems”, Austrian Society for Concrete and Construction, 2011.
5. Guidelines for the Design of Segmental Tunnel Linings, ITA-WG2, Tunnelling and Underground Space Technology, 2019.
6. Lining Segment Design: Recommendations for the Design, Production and Installation of Segmental Rings, German Tunnelling Committee, 2013.
7. T. Siwowski i in., Aspekty projektowania tunelu drogowego drążonego w technologii TBM w warunkach fliszu karpackiego, „Drogownictwo” nr 7–8/2022.
8. A.M. Muir Wood, The Circular Tunnel in Elastic Ground, „Géotechnique”, vol. 25, no. 1, 1975, s. 115–27.