Obliczanie i zbrojenie żelbetowych wsporników słupowych to dość złożone zagadnienie.
Wsporniki słupowe są często występującym, a jednocześnie bardzo odpowiedzialnym elementem konstrukcyjnym. Przekazują one na słupy obciążenia, np. od belek podsuwnicowych, belek stropowych czy rygli ściennych. Konieczność zastosowania wsporników może być także wymuszona np. przez formę budynku czy wymóg wprowadzenia do konstrukcji budynku dylatacji. W literaturze obcojęzycznej żelbetowe wsporniki słupowe występują pod następującymi określeniami: reinforced concrete corbel (ang.), Stahlbetonkonsole (niem.), console en beton arme (fr.).
Trochę historii
Żelbetowe wsporniki słupowe były od dawna obiektem zainteresowania wielu badaczy. W zależności od wysięgu wyróżnia się wsporniki długie (belki wspornikowe) i krótkie (zwane też krępymi). O ile sporne zagadnienia dotyczące wsporników długich zostały wyczerpująco wyjaśnione, o tyle poznania i wyjaśnienia wielu kontrowersyjnych aspektów ciągle wymagają wsporniki krótkie (które, pozornie proste i zewnętrznie statycznie wyznaczalne, stanowią jednak tak jak tarcze układy wewnętrznie statycznie niewyznaczalne). W Polsce badania eksperymentalne wsporników żelbetowych były prowadzone m.in. przez A. Zarzyckiego, A. Czkwianianca, S. Zakrzewskiego, K. Nagrodzką-Godycką.
Pierwszą koncepcję wymiarowania zarówno belek wspornikowych, jak i wsporników krótkich zawdzięczamy pracom E. Rauscha z lat 20. i późniejszych – z lat 50. (rys. 1). Zaproponowany przez Rauscha sposób obliczania wsporników panował niepodzielnie do początku lat 60. Dopiero w 1961 r. w swojej pracy doktorskiej radykalną zmianę sposobu projektowania wsporników żelbetowych zaproponował H. Niedenhoff, który nawiązując do przebiegu trajektorii naprężeń, zasugerował schemat dwugałęziowej kratownicy, w której pręty ukośne z modelu Rauscha zostały zastąpione jednym ukośnym ściskanym krzyżulcem wyodrębnionym z betonowego bloku wspornika (rys. 2).
Model zaproponowany przez Niedenhoffa był później modyfikowany przez wielu innych badaczy, m.in.: A. Mehmela i G. Beckera (1965), A. Zarzyckiego (1973), A. Czkwianianca (1974), G. Franza (1976), T. Hagberga (1983), J. Schlaicha (1984), A.S.G. Bruggelinga (1985). Zalecany obecnie przez Eurokod 2 schemat obliczeniowy wsporników krótkich to zmodyfikowany schemat kratownicy zastępczej wcześniej wprowadzonej do przepisów CEB-FIP (1993).
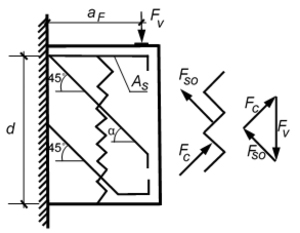
Rys. 1 Schemat krótkiego wspornika wg Rauscha (1922 r.)
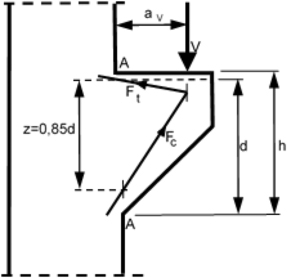
Rys. 2 Schemat krótkiego wspornika wg Niedenhoffa (1961 r.)
Obliczanie wsporników krótkich – metoda ST
Przy wymiarowaniu wsporników można korzystać z dwóch modeli obliczeniowych: analogii belkowej (wsporniki krótkie i długie) i analogii kratownicowej (tylko wsporniki krótkie). Euro- kod 2 nie narzuca sposobu wymiarowania wsporników, zaleca jednak stosowanie metody ST do wymiarowania wsporników krótkich.
Zgodnie z Eurokodem 2 wsporniki zaliczamy do krótkich, jeśli spełniony jest warunek:
ac < z0
gdzie: ac – odległość siły od krawędzi słupa; z0 – odległość od środka ciężkości przekroju zbrojenia głównego do punktu przecięcia osi krzyżulca ściskanego z krawędzią słupa.
Powyższe kryterium sprawdzić można niestety dopiero po określeniu wartości z0, a więc po zbudowaniu modelu ST (rys. 3).
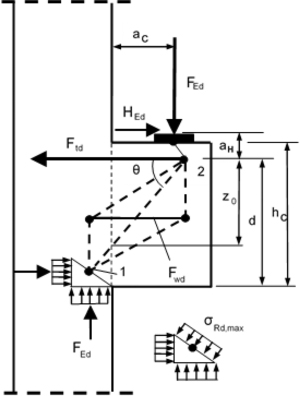
Rys. 3 Schemat obliczeniowy wspornika – metoda ST (wg Eurokodu 2)
Metoda ST (S – Strut – pręt ściskany, T – Tie – pręt rozciągany, cięgno) zwana jest też metodą zastrzałowo-cięgnową. Nowoczesność tej metody polega na zastosowaniu zasad teorii plastyczności i wykorzystaniu pewnych założeń odnoszących się do transferu sił z prętów zbrojeniowych na beton.
Model ST zawiera trzy różne elementy, które muszą być kontrolowane na etapie projektowania konstrukcji, są to: zastrzały (pręty ściskane), cięgna (pręty rozciągane) i węzły (miejsca, gdzie pręty się spotykają).
Pierwszym etapem projektowania jest ustalenie geometrii modelu obliczeniowego, który jest wpisany w kontur zewnętrzny analizowanego wspornika.
Przesunięcie górnego węzła układu prętowego względem osi siły FEd:
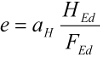
Zakłada się, że węzeł ściskany 1 jest tzw. węzłem hydrostatycznym – na wszystkich krawędziach strefy węzłowej ściskające naprężenie normalne jest równe σc.
Warunek równowagi momentów ze względu na punkt 1 (rys. 3):

Skąd wynika siła w zbrojeniu rozciąganym:
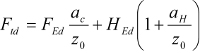
Węzeł 2 jest typu ściskanie – rozciąganie, z zakotwionymi w węźle prętami rozciąganymi w jednym kierunku. Warunek równowagi momentów ze względu na punkt 2 (rys. 3):

Skąd możemy wyznaczyć siłę w ściskanym krzyżulcu:

Sprawdzenie krzyżulca ściskanego:
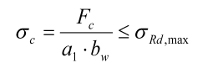
Naprężenie, które może być przyłożone do brzegów węzła, określa wzór (wartość współczynnika k2 w tym przypadku należy przyjmować równą 0,85):

W odniesieniu do krzyżulca między węzłami 1 i 2 można stosować wzór:
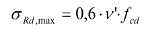
Szczegółową procedurę obliczania wsporników metodą ST (i przykłady obliczeniowe) znaleźć można np. w pozycjach [2], [6].
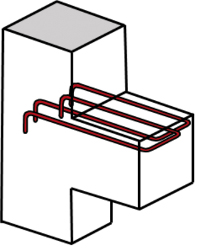
Rys. 4 Zbrojenie pętlami
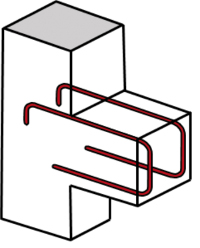
Rys. 5 Zbrojenie konturowe
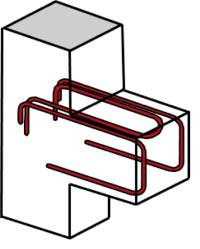
Rys. 6 Zbrojenie pętlami + konturowe
Obliczanie wsporników długich
Jeżeli wymaganie ac < z0 nie jest spełnione (wspornik długi), to do wymiarowania wspornika można wykorzystać znaną od dawna metodę belkową, stosowaną do wsporników krótkich i długich. W metodzie tej element się traktuje jak belkę wspornikową, a więc zbrojenie wymiaruje się na zginanie i ścinanie. Szczegółowy opis tej metody, a także przykłady obliczeniowe znajdują się np. w pozycjach [2], [6].
Porównując obie metody obliczeniowe (ST i belkową) w odniesieniu do wymiarowania wsporników krótkich (ac < z0), wyliczona potrzebna ilość zbrojenia jest mniejsza dla metody ST, metoda ta jest więc bardziej ekonomiczna, jeśli chodzi o zbrojenie.
|
Średnica pręta |
Minimalna średnica wewnętrzna haków prostych, haków półokrągłych i pętli |
|
Ø ≤ 16 mm |
4Ø |
|
Ø > 16 mm |
7Ø |
Konstruowanie zbrojenia wsporników
Zbrojenie główne
Norma Eurokod 2 wymaga, aby główne zbrojenie rozciągane krótkich wsporników było odpowiednio zakotwione na obu końcach. Długość zakotwienia zbrojenia wspornika w słupie należy odmierzać od pionowego zbrojenia słupa umieszczonego od strony wspornika, natomiast długość zakotwienia zbrojenia na końcu wspornika – od wewnętrznej krawędzi podkładki (płytki) przekazującej obciążenie. O ile z zakotwieniem zbrojenia w słupie z reguły nie ma większego problemu, o tyle zwykle kłopotów przysparza uzyskanie wymaganej długości zakotwienia na końcu wspornika.
W praktyce główne zbrojenie rozciągane wsporników kształtuje się w postaci pętli poziomych – rys. 4 (pętle mogą być pojedyncze lub podwójne) lub w formie zbrojenia konturowego – rys. 5 (pętli pionowych). Poprzednia norma żelbetowa w ogóle nie dopuszczała stosowania zbrojenia konturowego jako zbrojenia nośnego. Kotwienie za pomocą pętli poziomych jest korzystniejsze ze względów konstrukcyjnych (wymagane odległości od krawędzi wg 10.9.4.7 PN-EN). Z kolei zastosowanie zbrojenia konturowego powoduje, że nie są potrzebne dodatkowe pręty montażowe do chwycenia strzemion. Można też stosować te dwa typy zbrojenia jednocześnie (pręty konturowe na zewnątrz, jedna albo dwie pętle poziome w środku – rys. 6). Jeśli uzyskanie wymaganej długości zakotwienia na końcu wspornika jest problematyczne, to zastosować można zbrojenie zakotwione mechanicznie (dospawany poprzecznie na końcu zbrojenia kątownik – rys. 7, płaskownik albo jeden lub dwa pręty zbrojeniowe – rys. 8; produkowane są też fabryczne blokady mechaniczne, np. Halfen HSC – rys. 9).
Średnice zagięcia prętów kotwiących muszą być dobrane w taki sposób, aby nie mogło wystąpić miażdżenie betonu lub jego rozłupywanie. Przy kształtowaniu pętli muszą więc być spełnione warunki podane w tabl. 8.1 N PN-EN (patrz wyżej).
Spełnione musi być również wymaganie (wzór 8.1 PN-EN):
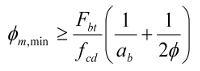
Jeśli zbroimy wspornik za pomocą pętli i okazuje się, że wyliczona minimalna średnica wewnętrzna zagięcia pętli sprawia, że w przyjętych gabarytach nie można umieścić dwóch pętli w jednej warstwie – to można umieścić też pętle w dwóch warstwach (rys. 10). W takim przypadku ulega jednak zmianie ramię sił wewnętrznych i konieczne jest ponowne przeliczenie wspornika.
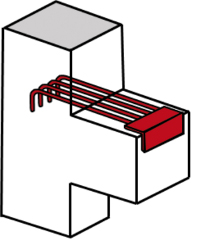
Rys. 7 Przyspawany kątownik
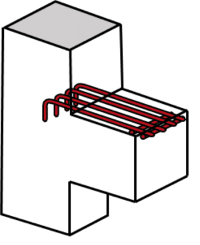
Rys. 8 Przyspawane pręty
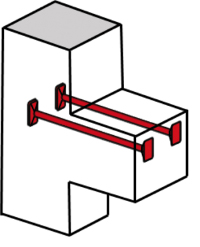
Rys. 9 Zbrojenie typu Halfen HSC
Zbrojenie uzupełniające (strzemiona)
W odniesieniu do wsporników krótkich Eurokod 2 przewiduje dwa sposoby zbrojenia uzupełniającego (w zależności od wysięgu ac).
Jeżeli ac < 0,5 hc, to należy zastosować zamknięte strzemiona poziome lub nachylone o przekroju As,lnk ≥ k1 As,main (wg załącznika krajowego do Eurokodu należy przyjmować k1 = 0,5). W takim przypadku model do obliczania zbrojenia uzupełniającego (wg [6]) i przykładowe zbrojenie wspornika wyglądają jak na rys. 11 i 12.
Ponieważ nie jest potrzebne zbrojenie poprzeczne (ścinanie przenosi sam beton), powinny być spełnione warunki (nośność na ścinanie):
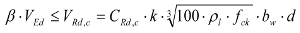
(wzór 6.2a wg PN-EN)
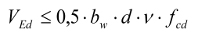
(wzór 6.5 wg PN-EN)
Jeśli ac > 0,5 hc i FEd > VRd,c, to należy zastosować zamknięte strzemiona pionowe o przekroju As,Ink ≥ k2 FEd/fyd (zalecaną wartością jest tutaj k2 = 0,5). Odpowiedni model do obliczania zbrojenia uzupełniającego (wg [6]) i przykładowe zbrojenie wspornika są przedstawione na rys. 13 i 14. Strzemiona pionowe potrzebne obliczeniowo rozkłada się na odcinku av. Należy zwrócić uwagę, że długość tego odcinka zależy od typu podkładki – dla podkładek twardych siła ścinająca przekazywana jest na krawędzi podkładki, natomiast dla podkładek miękkich przyjmuje się, że av = ac. Jeśli jest taka potrzeba, można zastosować strzemiona podwójne. Poza odcinkiem av stosuje się strzemiona konstrukcyjne.
Nośność na ścinanie jest sprawdzana wg wzorów:
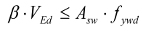
(wzór 6.19 wg PN-EN)
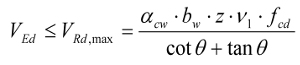
(wzór 6.9 wg PN-EN)
Przypadek, w którym FEd < VRd,cvv, nie został w Eurokodzie 2 uwzględniony. Według normy PN-B 03264:2002 należy wtedy stosować strzemiona pionowe o polu powierzchni wyliczonym wg wzoru:
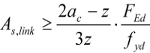
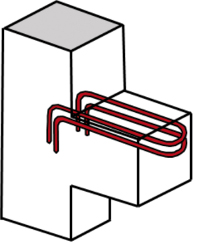
Rys. 10 Zbrojenie pętlami w dwóch warstwach
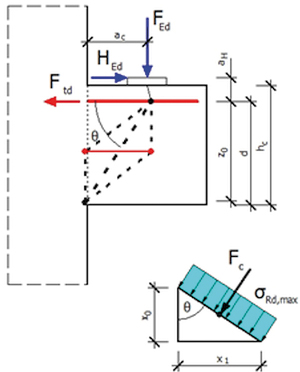
Rys. 11 I Model do obliczania zbrojenia uzupełniającego: ac < 0,5 hc
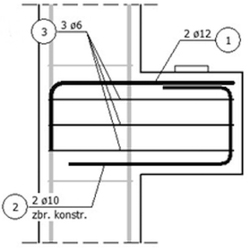
Rys. 12 I Przykładowe zbrojenie wspornika: ac < 0,5 hc
Zalecenia dotyczące zbrojenia wsporników
W niektórych opracowaniach znaleźć można zalecenie stosowania zbrojenia ukośnego (rys. 15). Rausch w swoich pracach zalecał stosowanie takiego zbrojenia, nachylonego do osi elementu pod kątem 45o. Dla odcinka belki równego wielkości ramienia sił wewnętrznych (z ≈ 0,85 d) należało zbrojeniem ukośnym przenieść siłę Fso = FV/√2, co prowadziło do zawyżenia ilości zbrojenia poprzecznego. Obecnie zarówno badacze, jak i projektanci preferują stosowanie strzemion pionowych, przy czym dla wsporników silnie obciążonych o znacznym wysięgu ramion, również zmienną wysokość wspornika (narastającą wraz ze zwiększającym się momentem). Projektowanie wsporników nie kończy się sprawdzeniem ich zdolności nośnej i konstruowaniem zbrojenia, ponieważ obciążone wsporniki wywołują również zakłócenia w sąsiadujących z nimi obszarach słupów. W miejscu wtopienia wspornika w słup powstają znaczne naprężenia rozciągające pionowe σy. Norma PN-B-03264:1999 wymagała, aby w tym miejscu zbrojenie przy- krawędziowe słupa miało powierzchnię przekroju poprzecznego nie mniejszą niż As (musiały być też spełnione warunki konstrukcyjne). Jeśli warunek ten nie był spełniony, należało przy krawędzi uzupełnić zbrojenie pionowe. Zdaniem W. Starosolskiego norma ta wprowadzała tutaj nadmierny zapas ilości zbrojenia, nawet w przypadku braku siły poziomej HEd. W Eurokodzie 2 nie ma już takiego wymagania. Według [5] konieczne jest jednak zagęszczenie strzemion w słupie bezpośrednio nad wspornikiem.
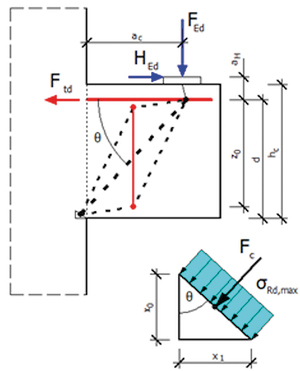
Rys. 13 Model do obliczania zbrojenia uzupełniającego: ac > 0,5 hc
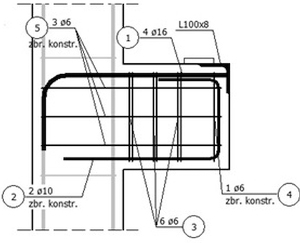
Rys. 14 Przykładowe zbrojenie wspornika, gdy ac > 0,5 hc
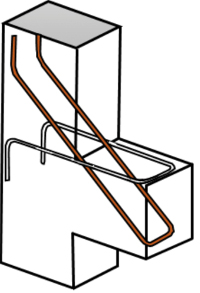
Rys. 15 Zbrojenie ukośne
Oprogramowanie komputerowe
Metoda obliczeniowa krótkich wsporników zalecana w Eurokodzie 2 (Strut & Tie) wymaga od projektanta bardzo dużego nakładu pracy i dużej staranności, co w codziennej praktyce inżynierskiej w zasadzie wyklucza obliczenia ręczne (konieczne jest korzystanie z arkuszy obliczeniowych i programów komputerowych). Na rynku oprogramowania inżynierskiego znaleźć można programy oparte na normie PN-B-03264:2002 (np. Kalkulator elementów żelbetowych firmy SPECBUD, Soldis Projektant), oraz takie oparte na Eurokodzie 2 (np. B9-krótki wspornik – Frilo Statik, wspornik słupowy wg PN-EN [1] – dlainzyniera.pl). Z czasem wybór oprogramowania będzie na pewno jeszcze większy.
Podsumowanie
Obliczanie i zbrojenie żelbetowych wsporników słupowych to złożone zagadnienie, którym powinni zajmować się raczej doświadczeni projektanci (konstruktorzy). Niezależnie od wyliczania potrzebnej ilości zbrojenia trzeba zawsze pamiętać o właściwym jego ukształtowaniu (także zbrojenia przylegającego do zbiornika obszaru słupa). Nie mniej ważne jest dobranie odpowiednich podkładek.
mgr inż. Jacek Gieczewski
PJG Konstrukcje Jacek Gieczewski
dlainzyniera.pl
Bibliografia
1. Norma PN-EN 1992-1-1 Eurokod 2: Projektowanie konstrukcji z betonu – Część 1-1: Reguły ogólne i reguły dla budynków.
2. M. Knauff, A. Golubińska, P. Knyziak, Tablice i wzory do projektowania konstrukcji żelbetowych z przykładami obliczeń,PWN, Warszawa 2014.
3. A. Łapko, B.C. Jensen, Podstawy projektowania i algorytmy obliczeń konstrukcji żelbetowych, Arkady, Warszawa 2005.
4. K. Zagrodzka-Godycka, Wsporniki żelbetowe. Badania, teoria, projektowanie, Wyd. Politechniki Gdańskiej, Gdańsk 2001.
5. W. Starosolski, Konstrukcje żelbetowe według Eurokodu 2 i norm związanych, tom III, wyd. IV, PWN, Warszawa 2012.
6. T. Urban, Przykłady projektowania żelbetowych wsporników,zeszyt 2, Wydawnictwo Politechniki Łódzkiej, Łódź 2012.