Stal budowlana w temperaturach pożarowych w świetle Eurokodów – cz. I

Wprowadzenie

W artykule tym podejmuję próbę odpowiedzi na pytania czytelników, którzy w następstwie moich poprzednich publikacji omawiających Eurokody projektowania konstrukcji obciążonych pożarem skierowali do mnie kilka listów. Zaliczyłem je do czterech kwestii szczegółowych:

1. Co wyrażają niejasne wzory (funkcje) na a, b i c w tablicy do rysunku 3.3 w normie PN-EN 1992-1-2, z czego one wynikają i jak je stosować.

2. Czy według Eurokodu PN-EN 1992-1-2 można sprawdzać bezpieczeństwo pożarowe istniejących konstrukcji z betonu zbrojonego stalami 34GS lub 18G2, wzniesionych w latach poprzednich, a obecnie rozbudowywanych lub modernizowanych.

3. Gdzie można znaleźć właściwości wytrzymałościowe tych stali w wysokich temperaturach pożarowych, zwłaszcza stali 34GS, której granica plastyczności wynosi ponad 400 MPa i w myśl Eurokodu PN-EN 1991-1-1, pkt 3.2.2 (3)P, można do niej stosować zalecenia Eurokodów.

4. Dlaczego przyjęto, że efektywna granica plastyczności stali konstrukcyjnej lub maksymalny poziom naprężeń stali zbrojeniowej w temperaturach aż do 400ºC są takie same jak w 20ºC? Czy nie ma tu pomyłki, bo przecież te wartości maleją wraz ze wzrostem temperatury, tak jak to uwzględniono przy zmianach granic proporcjonalności i modułu sprężystości liniowej?

Muszę od razu oznajmić, że do udzielenia odpowiedzi na takie pytania nie byłem i nie jestem uprawniony. Więcej, uważałem i nadal tak myślę, że pytania te powinny trafić do odpowiednich komitetów technicznych PKN, które opracowują polskie wersje tych norm europejskich, lub najlepiej do prawodawcy, który bierze udział w przygotowaniu załączników krajowych do Eurokodów i wprowadza te normy do obiegu prawnego oraz wymaga ich stosowania. W przedmowie do każdej części Eurokodu znajduje się informacja, którą można wyrazić słowami, że odpowiedzialność za zachowanie krajowego poziomu bezpieczeństwa konstrukcji pozostaje w gestii władz administracyjnych każdego z państw członkowskich, a poruszone kwestie, zwłaszcza w pkt 2, wymagają wykładni prawnej.

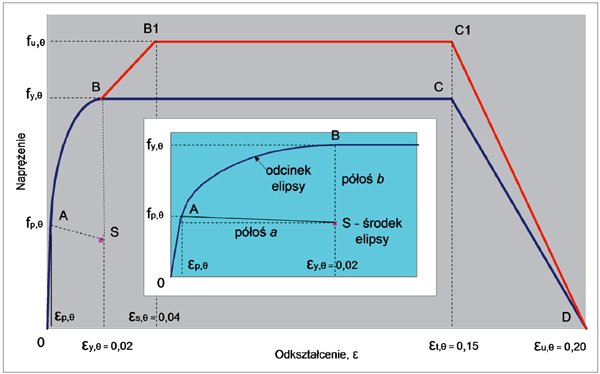
Rys. 1 Modele mechaniczne stali: podstawowy 0ABCD i alternatywny 0ABB1C1D ze wzmocnieniem w temperaturach poniżej 400ºC

Biorąc pod uwagę te ważne dla projektantów pytania, postanowiłem się podzielić posiadanymi wiadomościami, licząc, że inni czytelnicy dodadzą włas­ne uzupełnienia i sprostowania. Jest to przyczynek, do rozwinięcia tematu przez osoby bardziej biegłe w projektowaniu budynków na odporność ogniową. Aby zacząć, przystąpiłem do opracowania odpowiedzi na te pytania. Z dostępnych mi materiałów wybrałem badania właściwości mechanicznych stali 34GS i 18G2 w wysokich temperaturach pożarowych w latach 80. i  wyniki adaptowałem możliwie najlepiej do metodyki i oznaczeń przyjętych w normach PN-EC. Pragnę jednak uprzedzić, że artykuł ten jest wyłącznie poglądem autora.

W zbiorze Eurokodów istnieje pakiet ośmiu Polskich Norm przewidzianych do projektowania obiektów ze względu na warunki pożarowe, są to tzw. Eurokody pożarowe. Normy te mogą być stosowane także do sprawdzania konstrukcji w warunkach pożaru albo do oceniania ich stanu technicznego po pożarze. Jedna z norm odnosi się do podstaw projektowania, druga traktuje o oddziaływaniach pożaru na konstrukcje i sześć dotyczy konstrukcji  wykonanych z różnych materiałów. Wśród tych sześciu istnieją trzy, które dotyczą projektowania konstrukcji ze stali i do których nawiązuje ten artykuł. Są to:

– PN-EN 1992-1-2:2008 Eurokod 2: Projektowanie konstrukcji z betonu – Część 1-2: Reguły ogólne – Projektowanie z uwagi na warunki pożarowe;

– PN-EN 1993-1-2:2007 Eurokod 3: Projektowanie konstrukcji stalowych – Część 1-2: Reguły ogólne – Obliczanie konstrukcji z uwagi na warunki pożarowe;

– PN-EN 1994-1-2:2008 Eurokod 4: Projektowanie zespolonych konstrukcji stalowo-betonowych – Część 1-2: Reguły ogólne – Projektowanie z uwagi na warunki pożarowe.

Każda wymieniona norma, tj. część 1-2 Eurokodu 2, 3 lub 4, zawiera tylko wymagania odnoszące się do sytuacji wyjątkowej (realnie i obliczeniowo), jaką dla konstrukcji obiektu jest pożar, i powinna być stosowana łącznie z odpowiednią częścią 1-1, dotyczącą projektowania konstrukcji w warunkach normalnych. Warto dodać, że terminologia nie jest w nich ani jednoznaczna, ani ujednolicona, a oznaczenia są różne, co utrudnia odbiór i nie jest jedynym mankamentem tych norm. Po tak sążnistych dokumentach normalizacyjnych, których cel podstawowy ma prowadzić według definicji ustawowej „do uzyskania optymalnego stopnia uporządkowania”, można by oczekiwać większej zwięzłości i klarowności.

Do projektowania konstrukcji stalowych w temperaturze normalnej 20ºC są konieczne właściwości mechaniczne stali, do których należy zaliczyć trzy podstawowe cechy (różnie definiowane i oznaczane):

– nominalna (charakterystyczna) granica plastyczności (f_y);

– wytrzymałość na rozciąganie (f_t, f_u);

– moduł sprężystości (E_a, E_s).

Podczas pożaru wzrasta temperatura stalowych elementów konstrukcyjnych, pogarszają się ich właściwości wytrzymałościowe, zwiększa się ich odkształcalność, maleje, a nawet się wyczerpuje ich nośność. Obliczanie konstrukcji na wypadek pożaru powinno być prowadzone z uwzględnieniem zmian właściwości stali w funkcji temperatury według przyjętego modelu mechanicznego. Model ten został określony w Eurokodach, gdzie podano także zalecenia do obliczania konstrukcji obciążonej pożarem.

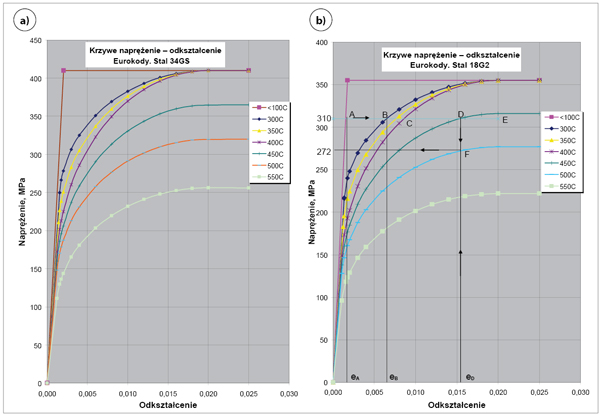
Rys. 2 Poglądowe wykresy zależności σ – ε wg modelu podstawowego w przedziale 0 ≤ ε ≤ 0,025 dla stali: a) 34GS przy f_y = 410 MPa; b) 18G2 przy f_y = 355 MPa (opis w tekście)

Model mechaniczny stali

Zacznijmy od pierwszego, najłatwiejszego pytania, tj. od kwestii dotyczącej parametrów a, b, c, które  występują w trzech wymienionych normach. Model mechaniczny stali, czyli zależność naprężenie–odkształcenie (s–e), przyjęty do projektowania zarówno konstrukcji żelbetowych, jak i stalowych oraz zespolonych stalowo-betonowych w warunkach pożaru, tj. w temperaturach do 1200ºC, imituje rzeczywiste wykresy naprężenie-odkształcenie uzyskiwane w próbie jednoosiowego rozciągania próbek w wysokich temperaturach. W Eurokodach stal jest traktowana w każdej temperaturze jako materiał idealnie sprężysto-plastyczny z fazą przejściową (rys. 1), z tym że w temperaturze do 100ºC nie przewiduje fazy przejściowej. Normy te, definiując model podstawowy, dodają do niego wariant/model alternatywny, w którym uwzględnia się umocnienie stali w temperaturach niższych od 400ºC. Model podstawowy ma zastosowanie do stali zbrojeniowej i konstrukcyjnej, model alternatywny można zastosować do obliczania konstrukcji stalowych i zespolonych stalowo-betonowych, pod warunkiem spełnienia dodatkowych wymagań podanych w PN-EN 1993-1-2:2007 i PN-EN 1994-1-2:2008.

Model podstawowy 0ABCD został zbudowany z czterech odcinków określonych za pomocą sześciu niezależnych parametrów. Składa się z:

– prostej 0A w zakresie liniowo sprężystym o stałym module sprężystości;

– łuku przejściowego AB w kształcie elipsy;

– prostej poziomej BC (półki plastycznej) w zakresie idealnie plastycznym;

– prostej opadającej CD.

Jest on opisany następującymi parametrami niezależnymi:

f_y,q– efektywna granica plastyczności stali w temperaturze q;

f_p,q– granica proporcjonalności stali w temperaturze q;

E_a,qlub E_s,q– moduł sprężystości liniowej stali w temperaturze q;

e_p,q= f_p,q/E_a,q– odkształcenie odpowiadające granicy proporcjonalności;

e_y,q= 0,02 – odkształcenie odpowiadające osiągnięciu granicy plastyczności;

e_t,q= 0,15 – odkształcenie przy końcu plastycznego płynięcia;

e_u,q= 0,20 – odkształcenie graniczne.

Model alternatywny to łamana 0ABB1C1D złożona z pięciu odcinków opisanych dodatkowymi dwiema wielkościami:

f_u,q– wytrzymałość na rozciąganie w temperaturze qz uwzględnieniem efektu umocnienia;

e_s,q= 0,04 – odkształcenie końcowe fazy umocnienia. 

W obu modelach występuje w każdej temperaturze wyższej od 100ºC łuk przejściowy AB. Ma on kształt (prawie) ¼ elipsy i jest styczny do prostej 0A w punkcie A, odpowiadającym granicy proporcjonalności f_p,q, i w punkcie B do prostej BC, odpowiadającym osiągnięciu efektywnej granicy plastyczności. Ponieważ wraz ze wzrostem temperatury maleją granica proporcjonalności f_p,qi efektywna granica plastyczności f_y,qoraz maleje kąt nachylenia prostej 0A (bo maleje moduł sprężystości), więc każdej temperaturze qodpowiada inny łuk elipsy, zawsze styczny do obu prostych w punktach A i B. W temperaturze do 100ºC punkt B nie zmienia swego położenia, jest na przedłużeniu prostej 0A. Osie elipsy są równoległe do osi współrzędnych s– e, a jej środek znajduje się w punkcie S, na prostej pionowej e_y,q= 0,02. Podane w normach parametry a i b to właśnie półosie elipsy. Wyższej temperaturze odpowiadają niższe położenie środka elipsy S i inne długości jej półosi. Stąd wynika wniosek, że a jest liczbą niemianowaną, b ma zaś wymiar naprężenia. Rozszyfrowaliśmy znaczenie symboli a i b.

Trochę trudniej odgadnąć znaczenie parametru c. Można to zrobić, jeśli równaniu elipsy w układzie współrzędnych s –e nadamy postać:

lub

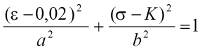
gdzie K = f_p,q– c jest właśnie rzędną środka S elipsy. Parametr c ma wymiar naprężenia i wskazuje, o ile niżej od f_p,qw modelu znajduje się punkt S. Znajomość znaczenia tych parametrów i ich wymiarów może być pomocna w kontroli obliczeń.

W tablicach Eurokodów (rozdział 3) podano związki między różnymi parametrami podstawowego modelu matematycznego stali zbrojeniowej i konstrukcyjnej. Dla modelu alternatywnego związki te zamieszczono w załącznikach A do PN-EN 1993-1-2:2007 i PN-EN 1994-1-2:2008. Zależności dla modelu podstawowego wyrażono w sposób ogólny za pomocą wprowadzonych wielkości odkształceniowych: e_y,q, e_t,qi e_u,q. Związki te pozostają ważne dla dowolnych wartości tych odkształceń. Ponieważ w Eurokodach przyjęto arbitralnie (z uzasadnieniem) wyżej wymienione wartości odkształceń i nie dopuszczono odstępstwa, dlatego wydaje mi się, że niepotrzebnie zachowano wzory w tak skomplikowanej postaci ogólnej, bo można było się obyć bez potrzeby wprowadzania parametru c. Pewnie autorzy norm mieli swoje racje, np. przewidując zmianę przyjętych wartości. Poza tym, gdyby wprowadzono do wzorów przyjęte wartości wyżej wymienionych odkształceń, wzory stałyby się prostsze i łatwiejsze do stosowania. W tabl. 1 podano wzory sprowadzone do postaci uproszczonej, a w tabl. 2 – zestawienie różnych oznaczeń parametrów opisujących model podstawowy według trzech Eurokodów pożarowych.

W modelu alternatywnym zaleca się przyjmować wytrzymałość na rozciąganie f_u,qz uwzględnieniem efektu umocnienia. Wyróżnia się tu dwa przedziały temperatury: poniżej 300ºC wytrzymałość ta jest równa 1,25 f_y,q, a w temperaturze od 300 włącznie do 400ºC spada liniowo do f_y,q (tabl. 1).

Tabl. 1 Związki między wielkościami mechanicznymi w modelu stali

Posługując się podanymi wzorami, można sporządzić dla stali o ustalonej granicy plastyczności f_y w temperaturze 20ºC wykresy zależności odkształcenie – naprężenie w różnych temperaturach qdla 0 ≤ e≤ 0,20, a w szczególności w przedziale odkształceń e_p,q≤ e≤ 0,02 (2%).

Do wyrażenia zależności między właściwościami stali w temperaturze normalnej i pożarowej q Eurokody wprowadzają trzy niezależne bezwymiarowe współczynniki redukcyjne:

– k_y,q= f_y,q/f_y – stosunek efektywnej granicy plastyczności w temperaturze qdo granicy plastyczności w temperaturze 20ºC, czyli współczynnik redukcyjny efektywnej granicy plastyczności;

– k_p,q= f_p,q/f_y – stosunek granicy proporcjonalności w temperaturze qdo granicy plastyczności w temperaturze 20ºC, czyli współczynnik redukcyjny granicy proporcjonalności;

– k_E,q= E_a,q/E_a lub E_s,q/E_s – stosunek modułu sprężystości w temperaturze qdo modułu sprężystości w temperaturze 20ºC, tj. współczynnik redukcyjny modułu sprężystości liniowej.

Wartości tych współczynników zostały ustalone i podane w postaci tabelarycznej i w formie wykresów w każdej z trzech części Eurokodów. Na tej podstawie można dla stali o określonej granicy plastyczności f_y w temperaturze normalnej wyznaczyć f_y,qi f_p,q oraz E_a,q, a następnie stosując wzory podane w tablicach, sporządzić wykresy s–edla różnych temperatur pożarowych. Odpowiednie wykresy przedstawiono na rys. 2, przyjmując z normy PN-H-84023/06 nominalne wartości granicy plastyczności stali 34GS i 18G2.

Pozostaje jeszcze uzupełnić odpowiedź na ostatnią część pierwszego pytania. Otóż mając wykresy s–e dla konkretnej stali w różnych temperaturach, możemy w razie potrzeby określić, jakie odkształcenia pojawią się w elemencie stalowym przy znanym naprężeniu i temperaturze lub, przeciwnie, jakim naprężeniom można go poddać, aby w przewidywanej temperaturze jego ekspozycji na ogień odkształcenia nie przekroczyły dopuszczalnej (przyjętej) wartości.

Tabl. 2 Różne oznaczenia parametrów opisujących model stali w Eurokodach

Posłużmy się w tym celu rys. 2b i przyjmijmy dla uproszczenia, że rozpatrujemy pręt ze stali 18G2 osiowo rozciągany naprężeniem s₁= 310 MPa (najprostszy stan wytężenia). Jego stan w temperaturze do 100ºC opisuje punkt A, któremu odpowiada doraźne odkształcenie sprężyste e_A. Po wzroście temperatury w czasie pożaru do 300ºC stan wytężenia przesuwa się do punktu B, położonego na przecięciu prostej poziomej dla s₁= 310 i krzywej s–edla 300ºC. Ten stan odkształcenia charakteryzuje odkształcenie doraźne e_B. Wzrost temperatury elementu do 450ºC przesuwa stan wytężenia do punktu D. Po osiągnięciu punktu E odpowiadającego granicy plastyczności w tej temperaturze (na wykresie nie ma tej krzywej) następuje płynięcie stali. Postępując w odwrotnej kolejności, możemy ustalić, że w temperaturze pożarowej 500ºC odkształcenie pręta nie przekroczy wartości e_D= 0,0155, jeśli naprężenie wyniesie co najwyżej 272 MPa.

Przedstawiona tu interpretacja ma charakter poglądowy, bo odnosi się do wyidealizowanego elementu konstrukcyjnego i jego prostego obciążenia. Nie oznacza to, że jest nieprzydatna. W sytuacjach realnych postępowanie jest bardziej złożone, nawet w przypadku zastosowania metod uproszczonych, i bez obliczeń w programach komputerowych trudno się obyć. W metodach uproszczonych chodzi raczej o odporność ogniową ze względu na noś­ność (kryterium R), ale są sytuacje, że jest konieczna znajomość odkształceń elementów w warunkach braku swobody.

mgr inż. Witold Ciołek

Bibliografia

1. M. Kosiorek, Charakterystyki mechaniczne stali budowlanych w podwyższonych temperaturach, Prace ITB nr 2(50), Warszawa 1984.

2. W. Ciołek, Praca naukowo-badawcza NP-18/7, Wyznaczanie charakterystyk reologicznych stali budowlanych w temperaturach wysokich wybranych gatunków stali budowlanych, M1.04.08.7, Opracowanie wynikowe nr 3, ITB, Warszawa 1985.

3. L. Runkiewicz, E. Wójcicka, St. Zakrzewski, Badania i ocena stali zbrojeniowej 34GS według norm zachodnioeuropejskich, „Inżynieria i Budownictwo” nr 11/1992.