Eurokod 3 – efektywne globalne projektowanie konstrukcyjne. Analiza oparta na modelu 3D przy użyciu ogólnej metody elementów skończonych belkowo-słupowych. Artykuł stanowi rozszerzenie tematu podjętego w „IB” nr 2/2011. Zawiera szczegółowy opis zwiększonych wymagań względem analizy modelu konstrukcyjnego.
Ogólny element belkowo-słupowy (MES)
Stopnie swobody i siły wewnętrzne
W projektowaniu używa się kilku rodzajów elementów skończonych. Element typu belka–słup jest osiowo ściskany i zginany względem osi y-y i/lub z-z przekroju. Element jest ogólny, jeżeli spełnione są następujące warunki:
– kształt przekroju ma charakter dowolny (otwarty lub zamknięty),
– ścianki przekroju są stosunkowo cienkie (cienkościenny przekrój poprzeczny),
– równania równowagi są geometrycznie nieliniowe i uwzględniają efekt deplanacji (efekt Wagnera).

Rys. 1. Lokalizacja wypadkowych naprężeń ogólnego elementu skończonego belkowo-słupowego
Powyższe warunki spełnia element Rajasekarana [3], który ma 14 stopni swobody. Rysunek 1 pokazuje układ lokalny i wypadkowe naprężenia elementu. Oś u zbiega do środka ciężkości, natomiast osie v oraz w to odpowiednio osie y-y i z-z przekroju. Wypadkowe naprężeń przy końcach j i k elementu są oznaczone jako:
N siła osiowa
Tv, Tw siły poprzeczne
Mv, Mw momenty zginające
Mu moment skręcający
B bimoment
Można zauważyć, że normalna siła i momenty zginające są rozpatrywane w środku ciężkości, podczas gdy siły poprzeczne, moment skręcający i bimoment w środku ścinania przekroju.
Przemieszczenia i naprężenia wypadkowe mogą być zapisane w postaci wektorowej:
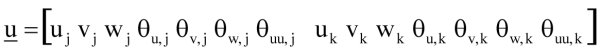
(1)
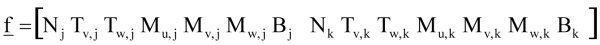
(2)
Macierzowe równania równowagi
Rajasekaran [1] stworzył macierzowe równania równowagi elementu ogólnego w klarownej formie,
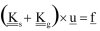
(3)
gdzie dotyczy zginania, a – sztywności geometrycznej. Macierze sztywności otrzymano z równania pracy wirtualnej elementu:
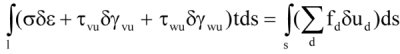
(4)
W równaniu (4) lewa strona wyraża pracę naprężeń wewnętrznych na odpowiednich odkształceniach wirtualnych, a prawa strona wyraża działanie sił powierzchniowych na odpowiednich przemieszczeniach wirtualnych. Z lewej strony l oznacza długość elementu, t jest odpowiednią grubością ściany, a s to współrzędna styczna. Ponadto σ = σu to naprężenie normalne, a σε to odpowiednie wirtualne odkształcenie normalne, z kolei τvu i τwu są składnikami naprężenia stycznego, a δεvu δεwu to odpowiednie wirtualne odkształcenia styczne w dowolnym punkcie elementu. Wskaźnik d po prawej oznacza stopnie swobody węzłów, tak jak to jest podane w równaniu (1).
Jednak Ks macierz sztywności przy zginaniu wyrażona jest w zakresie geometrycznych właściwości elementu, a Kg jest wyrażona w rzeczywistych wypadkowych naprężenia, takich jak
N siła osiowa
Tv, Tw siły poprzeczne (5)
Mv, Mw momenty zginające
Ponadto macierz sztywności geometrycznej zależy od współczynnika Wagnera, który można zapisać w następującej postaci ogólnej:
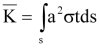
(6)
gdzie a jest odległością od obliczanego punktu przekroju do środka ścinania. Szczegóły można znaleźć na przykład w [3].
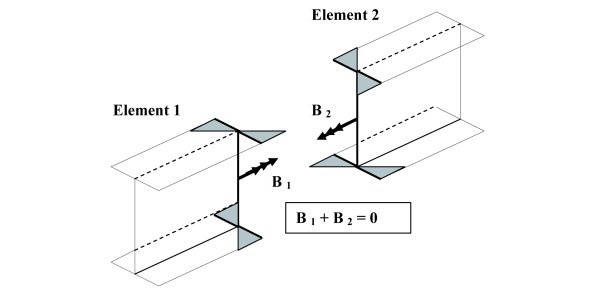
Rys. 2. Warunek zgodności dla deplanacji w połączeniach dla ogólnego modelu elementów skończonych
Tab. 1. Model schematu podparcia pręta konstrukcyjnego swobodnie podpartego (rys. 3)
|
Koniec pręta |
Stopnie swobody
|
||||||
|
u
|
v
|
w
|
θu
|
θv
|
θw
|
θuu
|
|
|
lewy
|
zablokowany
|
zablokowany
|
zablokowany
|
zablokowany
|
swobodny
|
swobodny
|
swobodny
|
|
prawy
|
swobodny
|
zablokowany
|
zablokowany
|
zablokowany
|
swobodny
|
swobodny
|
swobodny
|
Specjalne zdolności elementu ogólnego
Macierz sztywności geometrycznej tradycyjnego elementu 12 DOF (stopni swobody) odzwierciedla efekt siły osiowej na momenty zginające, ale pomija następujące efekty:
– interakcje między momentami zginania i skręcania,
– wpływ wypadkowego naprężenia osiowego na skręcanie (efekt Wagnera).
Element ogólny 14 DOF (stopni swobody) belkowo-słupowy jest geometrycznie nieliniowy (drugiego rzędu) i może uwzględniać powyższe efekty. Jednak ogólny element jest odpowiedni, aby obliczyć zachowanie skręcania według teorii Własowa. Praktycznie, używając tego elementu, możemy obliczyć zarówno efekt deplanacji, jak również postacie wyboczeń giętnych, skrętnych i zwichrzenia, a ponadto wszelkie interakcje pomiędzy tymi postaciami wyboczenia.
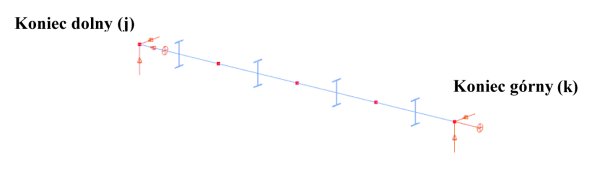
Rys. 3. Model elementów skończonych prętów swobodnie podpartych
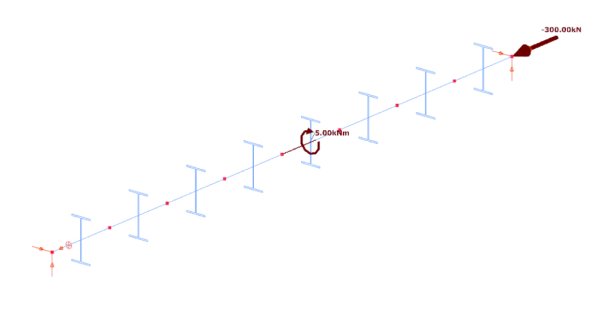
Rys. 4. Model skończonego elementu Beam7 pręta swobodnie podpartego, obciążonego przez moment skręcający i siły ściskające
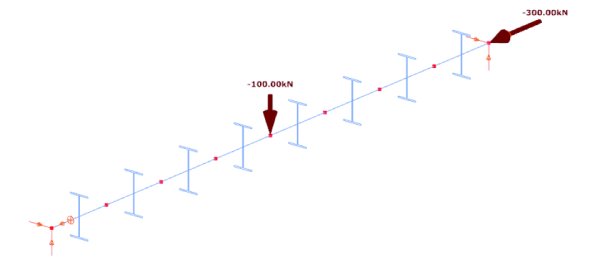
Rys. 5. Model skończonego elementu Beam7 pręta swobodnie podpartego, obciążonego przez siłę poprzeczną i ściskającą
Tab. 2. Szczegółowe wyniki analizy naprężeń
|
Analiza
|
Wyniki w środku przekroju
|
|||
|
θu (stopni)
|
B (kNm2)
|
σ?(N/mm2)
|
∑σu,max (N/mm2)
|
|
|
Pierwszy rząd – Beam7 – Shell3 |
5,843 5,854 |
5,040 – |
157.5 – |
197,1 196,1 |
|
Drugi rząd – Beam7 – Shell3 |
6,884 6,942 |
5,720 – |
178,7 – |
218,3 218,0 |
Analiza swobodnie podpartych prętów konstrukcyjnych
Warunek zgodności dla deplanacji
Zgodność deplanacji może być zapewniona przez następujące warunki w każdym węźle modelu elementu skończonego dla każdego pręta konstrukcyjnego (rys. 2):
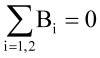
(7)
Równanie (7) zapewnia, że suma bimomentów (Bi) w połączeniach będzie równa zeru. Jeżeli przekrój jest jednorodny, a pręt prosty, metoda daje dokładne rozwiązanie.
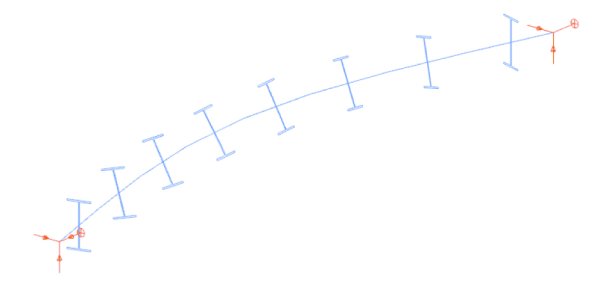
Rys. 6. Analiza stateczności globalnej modelu Beam7 (αcr= 1,42)

Rys. 7. Analiza stateczności globalnej modelu Shell3 (αcr= 1,40)
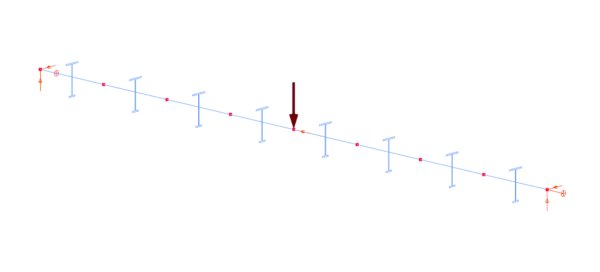
Rys. 8. Model Beam7 monosymetrycznej belki dwuteowej Mohriego (L = 6000 mm; obciążenie na środku ścinania; E = 210,000 N/mm2)
Tab. 3. Obliczone mnożniki obciążeń przy wyboczeniu
|
Metoda powłokowego elementu skończonego
|
αcr
|
|
Beam7
|
1,42
|
|
Shell3
|
1,40
|
Tab. 4. Krytyczne momenty wzorcowej belki Mohriego obliczone za pomocą różnych metod
|
Metoda
|
Krytyczny moment (kNm)
|
|
|
obciążenie działające w dół
|
obciążenie działające w górę
|
|
|
Ulepszona teoria*
|
77,48
|
54,65
|
|
Numeryczna (ABAQUS) **
|
77,41
|
53,99
|
|
Numeryczna (ConSteel) ***
|
77,98
|
53,83
|
|
* Ulepszone rozwiązanie teoretyczne. ** Numeryczne rozwiązanie z użyciem elementu powłokowego S8R5 oprogramowania ABAQUS. *** Za pomocą ogólnej FE belka–słup Rajasekarana. |
||
Modelowanie
Analizę naprężenia drugiego rzędu i analizę globalnej stateczności, która obejmuje wyboczenie skrętne jednorodnych prętów konstrukcyjnych, można przeprowadzić na podstawie prostego modelu, który zawiera od czterech do ośmiu ogólnych elementów skończonych belkowo-słupowych (rys. 3). W każdym węźle modelu jest 7 stopni swobody. Siódmy stopień teoretycznie oznacza pochodną kąta skręcania. Niemniej jednak każdy stopień swobody modelu może być zablokowany. Zasadniczo siódme stopnie (deplanacje) podparć modelu mogą być zablokowane (θuu = 0) lub mogą być swobodne jak standardowo. Model schematu podparcia pręta swobodnie podpartego 3D jest zdefiniowany w tab. 1.
Przykłady
Właściwości pręta konstrukcyjnego swobodnie podpartego są następujące:
– długość: 6000 mm,
– przekrój poprzeczny: spawany słup o przekroju dwuteowym (półki: 200-12; środnik: 412-8),
– moduł sprężystości: 210,000 N/mm2.
Najpierw obliczmy przemieszczenia i wypadkowe naprężeń pręta, który jest obciążony przez skupiony moment skręcający i stałe siły ściskające (przykład 1). Później obliczmy mnożnik obciążeń przy wyboczeniu pręta, który jest obciążony przez skupioną siłę poprzeczną i stałą siłę ściskającą (przykład 2). Przeanalizujmy modele, używając oprogramowania ConSteel [4], które wykorzystuje ogólny element Rajasekarana belkowo-słupowy, który opisano na początku artykułu. Oznaczymy ten element jako Beam7. W normalnych warunkach każdy pręt konstrukcyjny zostanie podzielony na osiem elementów skończonych. Sprawdzimy te analizy, używając niezależnych elementów skończonych powłokowych, gdzie skupimy się na geometrycznie nieliniowych trójkątnych elementach powłokowych z trzema węzłami. Oznaczymy ten element jako Shell3. Jednak będziemy używać końców utwierdzonych w modelach, aby uniknąć wyboczenia lokalnego oraz zniekształcenia. Na końcach zastosujemy płytki o grubości 2 mm, które mają pomijalny wpływ na analizę.
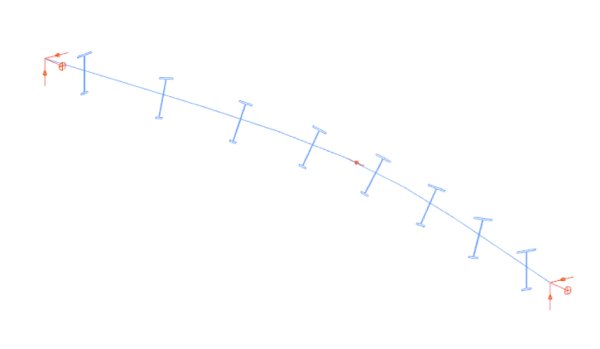
Rys. 9. Postać zwichrzenia belki dwuteowej monosymetrycznej I
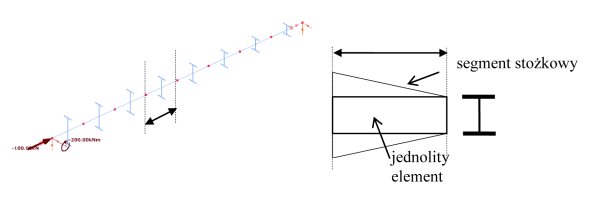
Rys. 10. Model Beam7 belki stożkowej (L = 6000 mm; obciążenie na centroidzie; E = 210,000 N/mm2)
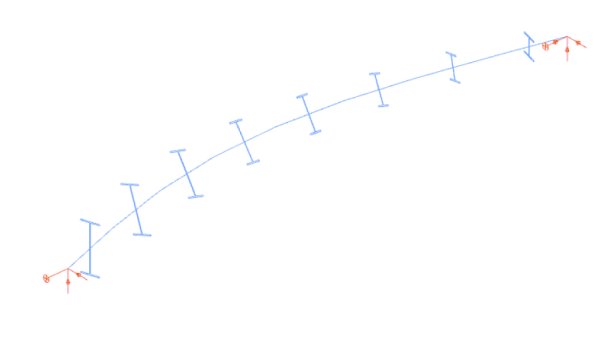
Rys. 11. Postać zwichrzenia belki dwuteowej stożkowej (αcr= 1,84)
Tab. 5. Mnożnik obciążeń przy wyboczeniu dla modeli stożkowych
|
Metoda
|
Mnożnik obciążeń przy wyboczeniu
|
|
Beam7 (ogólna metoda FE belka–słup z ośmioma elementami)
|
1,84
|
|
Shell3 (25 mm)
|
2,03
|
Przykład 1: Analiza naprężeń
Model obciążenia składa się z dwóch elementów: skupionego momentu skręcającego o wartości 5 kN przyłożonego w środku przekroju oraz ściskającej siły osiowej o wartości 300 kN na prawym końcu pręta (rys. 4). Szczegółowe wyniki analizy, którą przeprowadzono na modelu Beam7, przedstawiono w tab. 2. Przeanalizowano pręt konstrukcyjny przy użyciu modelu FE Shell3. Odpowiednie wyniki przedstawiono również w tab. 2.
Przykład 2: Analiza globalnej stateczności
Badamy ten sam pręt konstrukcyjny, który określono w przykładzie 1, ale model obciążenia składa się obecnie z obciążenia skupionego o wartości 100 kN działającego na środek pręta i osiowej siły ściskającej o wartości 300 kN (rys. 5). Analiza globalnej stateczności dostarcza wartość mnożnika obciążeń przy wyboczeniu i odpowiednią postać wyboczenia pręta (rys. 6). Tabela 3 to obliczone mnożniki obciążeń przy wyboczeniu, które obliczono na modelu ogólnym elementu skończonego belkowo-słupowego i modelu powłokowego elementu skończonego (rys. 7).
Analiza nieregularnych prętów konstrukcyjnych
Wykazaliśmy wcześniej, że ogólna metoda elementów skończonych belkowo-słupowych jest wystarczającym narzędziem do analizowania geometrycznie nieliniowego naprężenia i globalnej stateczności jednorodnych prętów konstrukcyjnych. Teraz pokażemy, że to narzędzie jest również wystarczające w analizie prętów o monosymetrycznym przekroju (przykład 3) i/ lub ze środnikiem (przykład 4).
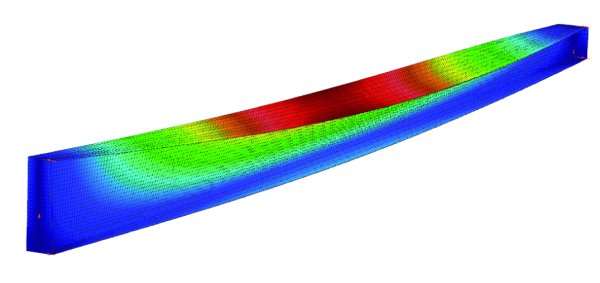
Rys. 12. Postać wyboczenia pręta otrzymana za pomocą metody elementów skończonych przy użyciu elementu Shell3 (αcr = 2,03)

Rys. 13. Efekt siły osiowej na element ekscentryczny
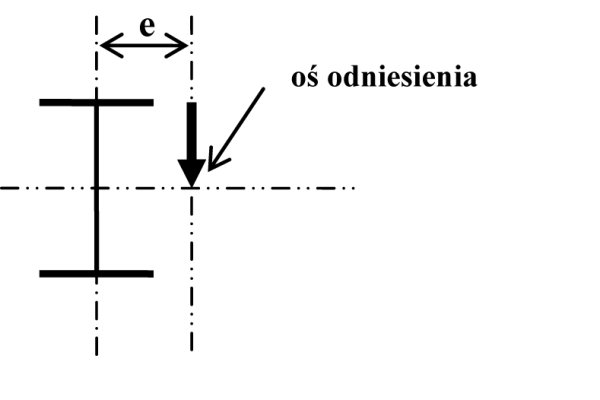
Rys. 14. Działanie siły poprzecznej na element mimośrodowy
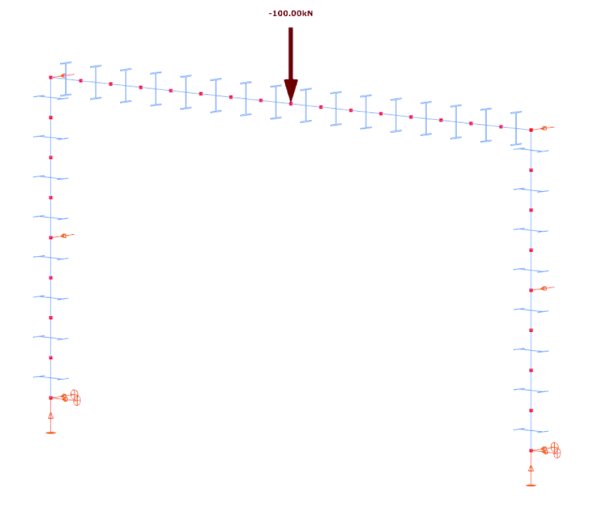
Rys. 15. Model Beam7 prostej konstrukcji ramy (zakres: 8000 mm; wysokość: 4000 mm; półki: 200-12; płyta środnika: 388-8; E = 210,000 N/mm2)
Przykład 3: Analiza globalnej stateczności prętów o monosymetrycznym przekroju dwuteowym
Efektywność ogólnej metody elementów skończonych belkowo-słupowych może być wykazana przez analizę globalnej stateczności monosymetrycznej belki swobodnie podpartej o przekroju dwuteowym, opublikowanej przez Mohriego i in. w [5]. Obliczyli oni moment krytyczny za pomocą ulepszeń teoretycznych oraz metod numerycznych (Abaqus). Rysunek 8 pokazuje model Beam7 ich wzorcowego przykładu, gdzie monosymetryczny słup o przekroju dwuteowym posiada półki 150/75-10,3 i środnik 289,3-7,1 (w zasadzie jest to uproszczony model przekroju IPE300). Rysunek 9 pokazuje postać zwichrzenia modelu. Tabela 4 przedstawia rozwiązanie Mohriego i numeryczne rozwiązania podane przez ogólną metodę FE belka–słup.
Przykład 4: Analiza globalnej stateczności stożkowych prętów konstrukcyjnych
Półki stożkowych prętów wykonane są z płyt 200-12; środnik jest wykonany z płyty 588/188-8, a długość pręta wynosi 6000 mm. Pręt podparty swobodnie jest obciążony przez moment zginający 200 kNm w płaszczyźnie symetrii i przez stałą siłę ściskającą 100 kN. Pręt jest zamodelowany za pomocą ośmiu jednolitych elementów ogólnych belkowo-słupowych (rys. 10). Wysokość elementu wynosi tyle, ile niższa wysokość segmentu. Mnożnik obciążeń przy wyboczeniu i postać wyboczenia zostały obliczone jako 1,84 (rys. 11). Obliczyliśmy mnożnik krytycznego obciążenia przy wyboczeniu również metodą elementów skończonych typu Shell3 (rys. 12). Metoda ta daje wartość 2,03 (tab. 5).
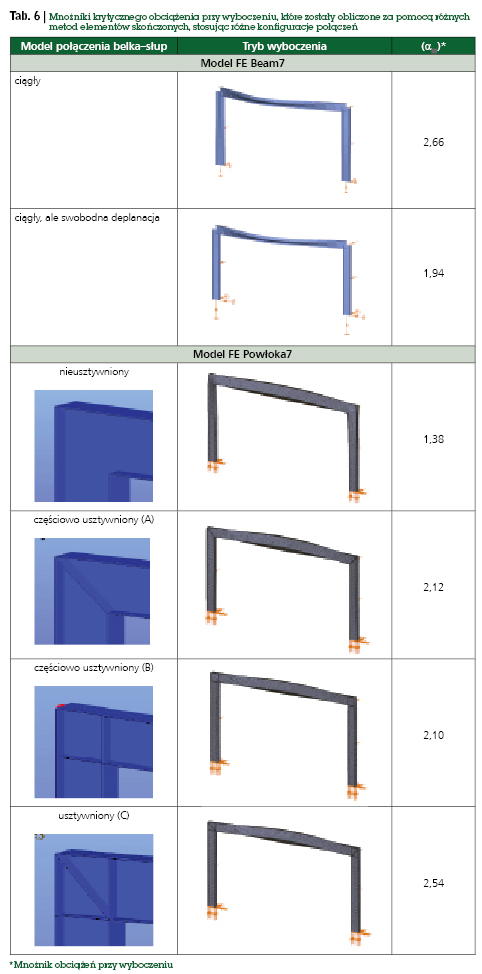
Tab. 6. Mnożniki krytycznego obciążenia przy wyboczeniu, które zostały obliczone za pomocą różnych metod elementów skończonych, stosując różne konfiguracje połączeń
Analiza złożonych struktur
Szczególne problemy modelowania
Przekształcenie deplanacji (spaczenia przekroju)
W bardziej skomplikowanej strukturze (np. ramie) pręty konstrukcyjne schodzące się w węźle są na różnych osiach odniesienia (np. połączeniu belka–słup). Jednak dla tych węzłów prawo opisujące przekształcenie deplanacji jest wyrafinowane, a ponadto w ramach teorii belek pozostaje ono nieznane. Aby wykorzystać ogólną metodę z użyciem elementów skończonych belkowo-słupowych do analizy bardziej złożonych struktur, możemy zastosować prosty warunek z równania (7). Przykład 5 pokazuje, że ten prosty warunek deplanacji daje akceptowalną analizę, jeśli łączenia konstrukcyjne są sztywne.
Mimośród obciążenia
Miejsce przyłożenia sił zewnętrznych w przekroju może drastycznie wpłynąć na mnożnik obciążeń przy wyboczeniu. Ogólny element skończony belkowo-słupowy osiągnięto, wychodząc z zasadniczego założenia, że siły ścinające przyłożone są w środku ścinania. W rezultacie w stanie wyjściowym modelu sił zewnętrznych siły te znajdują się w środku ścinania. Aby uwzględnić mimośród obciążenia, możemy połączyć punkt przyłożenia obciążenia i środek ścinania za pomocą fikcyjnego elementu. Fikcyjny element jest specjalnym i automatycznie generowanym elementem skończonym, który jest wystarczająco sztywny, aby przenieść efekty sił zewnętrznych, z wyjątkiem deplanacji.

Rys. 16. Model Beam7 stożkowej ramy

Rys. 17. Postać wyboczenia modelu Beam7 (αcr= 7,06)
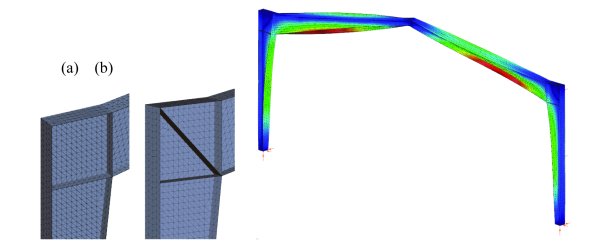
Rys. 18. Postać wyboczenia modelu Shell3 (αcr = 6,36) z żebrami wzmacniającymi w połączeniu belka–słup
Tab. 7. Szczegółowe wyniki analizy z użyciem różnych modeli
|
Metoda
|
Ugięcie w górnej części ramy (mm)
|
Mnożnik obciążeń
|
|
Beam7
|
14,48
|
7,06
|
|
Shell3 (50 mm) – usztywnienia środnika (a) – usztywnienie środnika i ścinania (b) |
12,64 12,17 |
6,52 9.66 |
Elementy mimośrodowe
Element skończony jest mimośrodowy, jeśli środek ciężkości jest poza jego osią odniesienia. Mimośrodowość może zostać wzięta pod uwagę w geometrycznej macierzy przekształceń elementu. Konsekwencją mimośrodowości jest dodatkowy moment zginający wynikający z siły osiowej (rys. 13) i zewnętrzny moment skręcający wynikający z poprzecznych siły zewnętrznych (rys. 14). Przykład 6 ilustruje sposób użycia elementu mimośrodowego, tak aby ustawić pręty stożkowe o przekroju dwuteowym górne lub dolne.
Przykład 5: Analiza globalna stateczności ram
Rysunek 15 przedstawia ogólny model elementu skończonego belkowo-słupowego prostej ramy, gdzie połączenia belka–słup są jednolicie sztywne (wskaźnik wytrzymałości połączeń belka–słup). Rama jest wsparta w kierunku poprzecznym na środku i na górze belki. Rama jest podpartą siłą skupioną o wartości 100 kN na środku belki. Obliczmy zatem mnożnik obciążeń przy wyboczeniu dla ramy za pomocą ogólnej metody z użyciem elementu skończonego belkowo-słupowego i uproszczonego stanu deplanacji podanego w równaniu (7). Jako element kontroli zastosowano model elementu skończonego Shell3 z różnymi rozwiązaniami konstrukcyjnymi dla połączeń belka–słup (od połączeń półsztywnych do połączeń sztywnych). Tabela 6 przedstawia mnożniki krytycznego obciążenia przy wyboczeniu, które zostały obliczone za pomocą różnych metod elementów skończonych, stosując różne konfiguracje połączeń. Możemy jednak przyjąć następujące wnioski:
– mnożnik krytycznego obciążenia przy wyboczeniu zależy od rodzaju konfiguracji połączenia belka–słup,
– wynik ogólnej metody elementów skończonych z użyciem elementów belkowo-słupowych jest bliski wynikowi metody elementów skończonych z użyciem elementów powłokowych, jeśli połączenie belka–słup jest usztywnione (sztywne).
Przykład 6: Modelowanie stożkowej konstrukcji ramy
Rozpiętość symetrycznej ramy stożkowej wynosi 12 000 mm (między osiami odniesienia słupów), a kąt nachylenia dachu – 10 stopni. Przekrój u podstawy belki i przy połączeniu belka–belka jest taki sam (spawany przekrój dwuteowy z półkami 200-12 i środnikiem 188/588-8). Obciążenia pionowe 10 kN/m jest rozłożone na osiach odniesienia belek. Rysunek 16 pokazuje model Beam7, rys. 17 – postać wyboczenia ramy, w której mnożnik krytycznego obciążenia przy wyboczeniu wynosi 7,06, natomiast rys. 18 pokazuje postać wyboczenia odpowiedniego modelu elementu skończonego powłokowego, gdzie mnożnik obciążeń przy wyboczeniu wynosi 6,36. Model powłokowy zawiera płyty podstwy o grubości 12 mm i żebra wzmacniające w połączeniach belka–słup oraz belka–belka. Tabela 7 przedstawia szczegółowe wyniki analizy uzyskane za pomocą różnych modeli.
Wnioski
Ogólny element skończony belkowo–słupowy został przedstawiony wcześniej. Analiza oparta na tym elemencie zawiera ogólne wypadkowe naprężenia drugiego rzędu w zakresie sprężystym drugiego rzędu. Te wypadkowe naprężenia są niezbędne do kompleksowej oceny wytrzymałości dowolnego przekroju poprzecznego regularnych i nieregularnych prętów konstrukcyjnych. Analiza globalnej stateczności w zakresie sprężystym na podstawie tej metody pozwala wyznaczyć mnożnik obciążeń przy wyboczeniu, który jest istotnym parametrem w metodzie ogólnej w zakresie wytrzymałości w płaszczyźnie prętów konstrukcyjnych i elementów konstrukcyjnych. Metoda ta jest dopuszczalna, gdy dominującą postacią jest wyboczenie skrętne lub interakcja wyboczenia giętnego oraz wyboczenia skrętnego. Może być z powodzeniem wykorzystywana do nieregularnych prętów konstrukcyjnych i przekrojów. W niniejszym artykule wykorzystano oprogramowanie do projektowania konstrukcyjnego ConSteel w celu zilustrowania efektywności ogólnej metody projektowania, wykorzystując ogólną metodę analizy elementów skończonych belkowo-słupowych.
dr Ferenc Papp
prof. Wydziału Inżynierii Konstrukcyjnej, BUTE, Węgry
dr József Szalai
główny pracownik naukowy,
ConSteel Solutions Ltd, Węgry
konsultacje:
mgr inż. Lech Ciesielski
inż. Iwona Janus
Biuro tłumaczeń: ALLENA
Bibliografia
1. EN 1993-1-1 Eurokod 3: Projektowanie konstrukcji stalowych – Część 1.1: Reguły ogólne i reguły dla budynków, 2005.
2. EN 1993-1-5 Eurokod 3: Projektowanie konstrukcji stalowych – Część 1.5: Blachownice, 2006.
3. W.F. Chen, T. Atsuta, Theory of Beam-Columns: Space behavior and design, t. 2, McGraw-Hill, 1977.
4. www.consteel.hu
5. F. Mohri, A. Brouki, J.C. Toth, Theoretical and numerical stability analyses of unrestrained, mono-symmetric thin-walled beams, „Journal of Constructional Steel Research” 59/2003.