Ilościowe aspekty zastosowania termowizji w budownictwie

Problem oceny stanu izolacji budynków i ilościowe wyznaczanie wartości współczynnika przenikania ciepła U nie jest łatwym zadaniem. Istnieje kilka inżynierskich metod wyznaczania wartości U, są rekomendacje w normach, a mimo to błędy oceny stanu izolacji w budownictwie są znaczne.

Współczynnik przenikania ciepła

Definicja współczynnika przenikania ciepła U dla przegród budowlanych oraz zasady jego wyznaczania precyzuje norma PN-91/B-02020 [1]. Według tej definicji jest to parametr, który zależy od oporów wnikania ciepła do przegrody, oporów przewodzenia w przegrodzie oraz od warunków odprowadzania ciepła do otoczenia.

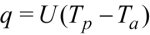
(1)

gdzie: T_p oznacza temperaturę w pomieszczeniu, a T_a – temperaturę powietrza na zewnątrz, z dala od budynku.

Można oszacować wartość współczynnika U na podstawie pomiarów temperatury dla ściany zewnętrznej i wewnętrznej. W tych przypadkach wymagana jest znajomość współczynników przejmowania ciepła zarówno dla ściany zewnętrznej, jak i wewnętrznej α_z, α_w. Zakłada się przy tym jednowymiarowy przepływ ciepła przez przegrodę i równość strumienia wpływającego do przegrody z pomieszczenia i odprowadzanego do otoczenia. Niezgodność tych strumieni świadczy o błędach w pomiarze temperatury, niewłaściwym oszacowaniu współczynników przenikania ciepła lub rozpływie ciepła w przegrodzie, co wynika np. z niejednorodności przegrody, wentylacji w przegrodach wielowarstwowych lub nieciągłości izolacji cieplnej i obecności mostków termicznych. Biorąc pod uwagę możliwość wyznaczenia wartości współczynnika U przy pomiarze temperatury po wewnętrznej i zewnętrznej powierzchni przegrody, można przedstawić kilka równoważnych zależności opisujących współczynnik U [2–5]

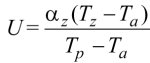
(2)

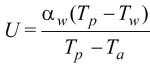
(3)

(4)

gdzie: α_w i α_z to współczynniki wnikania i przejmowania ciepła przegrody na styku z otoczeniem, wewnątrz i na zewnątrz budynku; T_w i T_z – wartości temperatury po stronie wewnętrznej i zewnętrznej przegrody.

Praktyka badań termowizyjnych obiektów budowlanych potwierdza, że oszacowanie wartości współczynnika α_w jest dokładniejsze niż α_z, co wynika głównie ze zmiennych warunków atmosferycznych. W rozważaniach pominięto ponadto wpływ promieniowania słonecznego oraz wpływ na α_z takich parametrów, jak wilgotność i ciśnienie, które niewątpliwie mogą zmienić wartość współczynnika przejmowania ciepła.

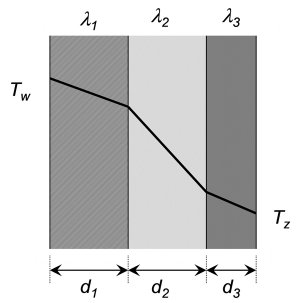
Rys. 1. Rozkład temperatury w przegrodzie trójwarstwowej

Rezystancja termiczna przegrody budowlanej

Jak wspomniano wcześniej, współczynnik przenikania ciepła U uwzględnia trzy zjawiska przekazywania ciepła przez przegrodę, tj. wnikanie, przewodzenie i odprowadzanie do otoczenia. Przedstawione wyżej rozważania pozwalają ocenić, jaki jest udział każdego z nich i identyfikację słabego (w sensie znacznej wartości oporu cieplnego) ogniwa w łańcuchu trzech oporów termicznych, przez które ciepło ucieka do otoczenia.

Rozważmy strukturę wielowarstwową jak na rys. 1. Opór termiczny ma różne definicje, czasem odnosi się do jednostkowej powierzchni badanego obiektu, czasem dotyczy obszaru o określonej wielkości. W budownictwie przyjmuje się ujednolicone opory termiczne wyznaczone dla jednostkowej powierzchni. Ogólnie rezystancję termiczną przegrody R_th w zależności od wewnętrznego współczynnika przejmowania ciepła przedstawia równanie

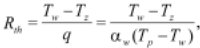
(5)

przy czym q jest strumieniem ciepła (a dokładnie mocy) w W/m², przekazywanym do otoczenia przez przegrodę w warunkach ustalonego przepływu ciepła.

Rezystancja termiczna przegrody R_thp z rys. 1 jest funkcją parametrów cieplnych i rozmiarów przegrody i ma postać

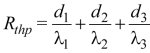
(6)

gdzie: d_i, λ_i są grubością i przewodnością termiczną danej warstwy.

Analogicznie rezystancje termiczne na styku ośrodka i przegrody można przedstawić następująco

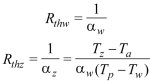
(7)

gdzie R_thw i R_thz oznaczają opory termiczne na styku ściany wewnętrznej i zewnętrznej z otoczeniem.

Ciepło przenika przez przegrodę oraz przez jej wewnętrzną i zewnętrzną płaszczyznę tą samą powierzchnią (model jednowymiarowy). W takim przypadku rezystancje termiczne są połączone szeregowo (rys. 2) i sumują się

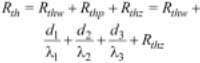
(8)

gdzie R_thp jest oporem termicznym przegrody.

Rys. 2. Opory termiczne przegrody budowlanej i otoczenia

Współczynnik przenikania ciepła U można ostatecznie wyrazić jako

(9)

Zgodnie z oczekiwaniami największy udział w całkowitym oporze cieplnym ma przegroda, a najmniejszy warstwa powietrza po zewnętrznej stronie budynku. Jest to zrozumiałe, ponieważ silne odprowadzanie ciepła do otoczenia na zewnątrz budynku wynika z wymuszonego chłodzenia konwekcyjnego. Wyznaczona wartość oporu cieplnego przegrody na podstawie pomiarów jej temperatury i otaczającego ośrodka, przy założeniu typowych wartości współczynników przenikania ciepła na krawędziach przegrody, może być zweryfikowana z danymi konstrukcyjnymi budynku według równania (6).

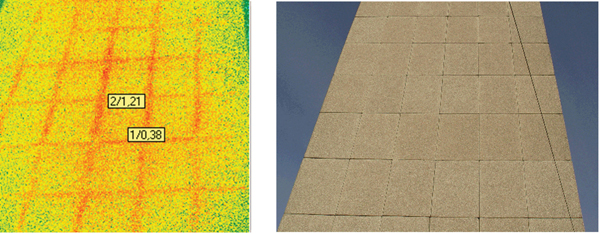
W przykładzie przedstawiono trójwarstwową przegrodę budowlaną z rys. 1. Przyjęto następujące parametry warstw:

– d₁= 0,188 m, λ₁ = 0,5 W/(m·K) – cegła ceramiczna,

– d₂= 0,10 m, λ₂ = 0,04 W/(m·K) – styropian,

– d₃= 0,088 m, λ₃ = 0,5 W/(m·K) – cegła ceramiczna.

Wartości składowych oporu cieplnego trójwarstwowej przegrody budowlanej zawarte są w tab. 2.

Biorąc jednak pod uwagę uproszczony charakter oszacowania wartości współczynników przejmowania ciepła przez konwekcję i współczynnika emisyjności, można stwierdzić, że wartość rzeczywista współczynnika U będzie nie mniejsza od wartości obliczonej. Przy założeniu jednowymiarowego przepływu ciepła przez przegrodę wartości strumieni ciepła i współczynników U wyznaczone na podstawie równań (2) i (3) po obu stronach przegrody budowlanej powinny być jednakowe. W praktyce mogą się różnić, co oznacza, że można wyznaczyć wartość średnią współczynnika U dla pomiarów na zewnątrz i wewnątrz budynku.

Rys. 2. Rozkład temperatury w przegrodzie trójwarstwowej

Mostki termiczne

Termowizja w budownictwie jest stosowana także do wykrywania mostków termicznych. Często zadawane jest pytanie, czy i kiedy udział mostków termicznych jest znaczący w bilansie strat energii cieplnej w budownictwie?Rozważmy proste przykłady przedstawione na rys. 2 i 3. Istnienie mostków termicznych można łatwo zlokalizować za pomocą obrazu termowizyjnego zewnętrznej ściany budynku. Mostki termiczne bez wątpienia zwiększają straty energii, gdyż lokalna wartość temperatury w określonych miejscach przegrody budowlanej jest większa. Wzrost wartości temperatury powoduje wzrost zarówno strumienia radiacyjnego, jak i konwekcyjnego, którymi ciepło ucieka do otoczenia.

Wzrost strumienia mocy wyrażonego w W/m² jeszcze o niczym nie świadczy. Ważna jest powierzchnia, przez którą mostek termiczny rozprasza ciepło do otoczenia i którą łatwo można oszacować z termogramów (rys. 2 i 3). Załóżmy, że powierzchnia zajmowana przez wszystkie mostki termiczne wynosi około 5% całej powierzchni przegrody, a temperatura przegrody na zewnątrz budynku w miejscu mostka termicznego jest większa zaledwie o 1 ºC od dobrze izolowanej części budynku. W takim przypadku przykładowy odział strumieni i mocy cieplnej przenikających przez przegrodę i mostek termiczny przedstawiono w tab. 3.

Tab. 1. Przykładowe opory cieplne i współczynniki przejmowania ciepła trójwarstwowej przegrody budowlanej: d₁ = 0,188 m, λ₁ = 0,5 W/(m?K), d₂ = 0,10 m, λ₂ = 0,04 W/(m?K), d₃ = 0,088 m, λ₃ = 0,5 W/(m?K), v = 5 m/s

Tab. 2. Składowe oporu cieplnego przegrody budowlanej otrzymane z równania (6)

Tab. 3. Strumienie ciepła, powierzchnie oraz ciepło przenikające przez przegrodę, mostek termiczny ma wymiary zgodne z modelem w [3]

W praktyce istnieje wiele małych (w sensie powierzchni) mostków termicznych, których udział w całkowitym bilansie strat ciepła może być pominięty.Należy jednak pamiętać, że mostki termiczne stanowią inne, duże zagrożenie badanego budynku. Mogą stanowić miejsce, gdzie będą przebiegać procesy erozji biologicznej i fizykochemicznej. Ze względu na podwyższoną wartość temperatury mostka termicznego może tu zachodzić kondensacja pary wodnej, zawilgocenie, zagrzybienie i zmiany strukturalne przegrody (pęknięcia, wykruszenia itp.).

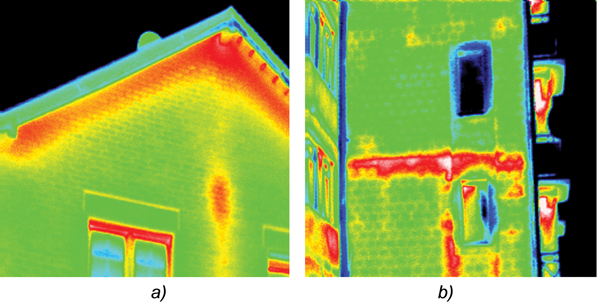
Rys. 3. Rozkład temperatury na ścianie budynku: a) jednorodzinnego – pionowy mostek wnikający z braku izolacji poprzecznej ściany działowej; b) wielorodzinnego – mostek termiczny stropu między kondygnacjami

Efekty na krawędziach

W praktycznych badaniach termowizyjnych budynków można zauważyć zmianę wartości lokalnego współczynnika przenikania ciepła na wklęsłych i wypukłych krawędziach konstrukcji. Jest to typowy i normalny z fizycznego punktu widzenia efekt geometryczny. Na wklęsłej krawędzi zewnętrznej obserwuje się zwiększenie wartości temperatury ze względu na większą powierzchnię przegrody na stronie wewnętrznej i mniejszą po stronie zewnętrznej – rys. 3. Odwrotna sytuacja ma miejsce dla krawędzi wypukłej. Wewnątrz budynku kamera termowizyjna zarejestruje na krawędzi wklęsłej wyraźny spadek wartości temperatury – rys. 4. Ocena wartości współczynnika przenikania ciepła na krawędziach jest trudna i nie jest zalecana. Można próbować ocenić ciągłość izolacji w tych miejscach. Do tego celu należy wykorzystać modele termiczne przegrody. Wyniki obliczeń przedstawią oczekiwaną wartość spadku/wzrostu wartości temperatury na krawędzi w zależności od konstrukcji przegrody, jej grubości i  warunków otoczenia. Zdecydowanie lepiej wykonać taką ocenę wewnątrz budynku ze względu na ustabilizowane warunki wymiany ciepła. Jakościowo stan izolacji na krawędzi można ocenić przez analizę kształtu krzywej termicznej i jej zmian w różnych punktach krawędzi. W przypadku ciągłej izolacji na krawędzi charakter zmian temperatury powinien być zbliżony do krzywej ekspotencjalnej [6] i krzywa ta powinna być prawie taka sama dla niemal całej krawędzi z pominięciem obszarów przy podłodze i suficie.

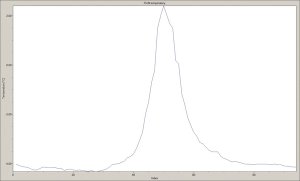
Rys. 4. Wzrost temperatury na wklęsłej krawędzi budynku

Wyznaczanie wartości współczynnika przenikania ciepła U

Do wyznaczenia wartości współczynnika przenikania ciepła U dla przegród budowlanych metodą termograficzną opracowano arkusz kalkulacyjny. Zastosowano równania (1) i (2) do obliczenia współczynników przejmowania ciepła oraz strumieni ciepła odpowiednio dla ściany wewnętrznej i zewnętrznej. Dla przegrody termicznej, przez którą strumień ciepła przepływa jedynie w kierunku poprzecznym (model jednowymiarowy, brak rozpływu ciepła w przegrodzie), współczynnik U według normy [3] zdefiniowany jest równaniem

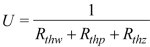
(10)

gdzie: R_thz,R_thw,R_thp oznaczają opory termiczne ścian budynku zewnętrznej i wewnętrznej oraz opór samej przegrody.

Ponieważ taki sam strumień q przenika przez wszystkie elementy przegrody i otoczenie wewnątrz i na zewnątrz przegrody, założono wyznaczanie wartości współczynnika U po obu jej stronach i obliczenie wartości średniej

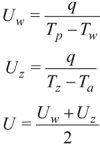
(11)

przy czym: T_p, T_w, T_z i T_a to wartości temperatury w pomieszczeniu, po wewnętrznej i zewnętrznej stronie ściany oraz otoczenia.

Głównym problemem pomiarowym staje się więc wyznaczenie wartości całkowitego strumienia przenikania mocy przez przegrodę q. W praktyce pomiarowej można jego wartość oszacować na podstawie parametrów modeli termicznych dla ściany zewnętrznej i wewnętrznej, a uzyskane wyniki uśrednić (równanie 4). Opracowany pakiet do wyznaczania wartości współczynnika U zawiera moduł szacowania strumienia ciepła zarówno po stronie wewnętrznej, jak i zewnętrznej przegrody.

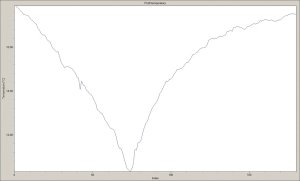
Rys. 5. Spadek wartości temperatury na wklęsłej krawędzi przegrody wewnątrz budynku

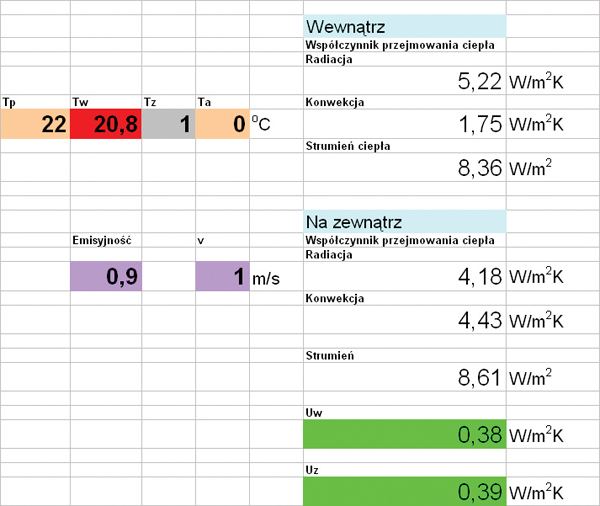
Rys. 6. Arkusz kalkulacyjny do wyznaczania wartości współczynnika przenikania ciepła U przez przegrody budowlane

Wnioski

Termowizyjna metoda pomiaru współczynnika przenikania przez przegrody budowlane jest w Polsce i na świecie coraz bardziej wykorzystywana w praktyce. Metoda ta daje niemal natychmiastowy wynik rozkładu wartości lokalnego współczynnika przejmowania ciepła na dużej powierzchni przegrody. Jest bezdotykowa, można za jej pomocą badać wyższe kondygnacje budynków, ale wymaga wiedzy i doświadczenia operatora w celu właściwej interpretacji uzyskanych wyników.

Badania termowizyjne w budownictwie należy prowadzić we właściwych warunkach środowiskowych:

– brak opadów,

– mała wilgotność powietrza,

– bezwietrzna pogoda,

– znaczna różnica temperatury wewnątrz i na zewnątrz budynku,

– brak nasłonecznienia (najlepiej przed świtem),

– z uwzględnieniem promieniowania podstawy chmur lub nieboskłonu.

Należy podkreślić, że w badaniach ilościowych w budownictwie zakładamy jednokierunkowy przepływ ciepła, co nie zawsze jest do spełnienia. Jeśli występują poprzecznie mostki termiczne i ciepło rozpływa się wewnątrz przegrody, to wyniki pomiarów mogą być błędne. Podczas badań termowizyjnych zalecana jest identyfikacja emisyjności przegrody budowlanej. Nie należy wykonywać pomiarów metalowych lub szklanych elementów konstrukcyjnych budynku. Ze względu na nie do końca określone warunki oddawania ciepła do otoczenia na zewnątrz budynku zdecydowanie zaleca się pomiary wartości współczynnika U wewnątrz. Wydaje się, że połączenie metody termowizyjnej ze stykową jest najlepszym rozwiązaniem. Stosowanie kamery termowizyjnej i miernika strumienia ciepła do punktowych pomiarów energetycznych może wpłynąć na zwiększenie dokładności wyznaczania wartości współczynnika U.

prof. Bogusław Więcek

mgr inż. Robert Strąkowski

Instytut Elektroniki, Politechnika Łódzka

Literatura

Polska Norma PN-91/B-02020.

2. A. Wróbel, Termograficzne badanie izolacyjności cieplnej budynków, konferencja Termografia i termometria w podczerwieni, Łódź 2000.

3. B. Więcek, G. De Mey, Termografia w podczerwieni, podstawy i zastosowania, Wydawnictwo PAK, Warszawa 2011.

4. A. Wróbel, Termografia w pomiarach inwentaryzacyjnych obiektów budowlanych, Wydawnictwa AGH, 2010.

5. B. Więcek, Wybrane zagadnienia współczesnej termowizji w podczerwieni, Politechnika Łódzka, Łódź 2010.

6. G. De Mey, B. Więcek, I. Papagiannopoulos, V.  Chatziathanasiou, Influence of geometrical effects on the wall corner temperature in buildings, „PAK” nr 10/2011.