Wszystko, co chcielibyśmy wiedzieć, ale boimy się zapytać – cz. II.
Uwagi dotyczące załącznika C (informacyjnego) „Podstawy współczynników częściowych i analizy niezawodności”
1. Tytuł załącznika C byłby bardziej czytelny, gdyby brzmiał następująco: „Podstawy projektowania opartego na częściowych współczynnikach bezpieczeństwa oraz podstawy analizy konstrukcji pod względem niezawodności” (zgodnie z [2]).
2. Zamiast terminu „prawdopodobieństwo zniszczenia” zastosowanego w odniesieniu do Pf (s. 48 i dalsze) lepiej byłoby użyć terminu „prawdopodobieństwo awarii” (ang. probability of failure). Przez pojęcie „awaria” rozumie się przekroczenie przez element konstrukcyjny danego stanu granicznego, co nie jest równoznaczne z jego zniszczeniem.
3. Zamiast terminu „funkcja rozkładu prawdopodobieństwa standaryzowanego rozkładu normalnego” zastosowanego w odniesieniu do Φ (s. 48 i dalsze) powinien być użyty termin „dystrybuanta rozkładu normalnego standaryzowanego”.
4. Zamiast terminu „punkt obliczeniowy” (s. 52) lepiej byłoby użyć „punkt projektowy” (zgodnie z [2]), ponieważ wartości obliczeniowe nośności i efektów obciążenia przyjęte przy wymiarowaniu nie zawsze są równe współrzędnym punktu projektowego.
5. W punkcie C3(1) nie chodzi o „nośność”, lecz o „wytrzymałość”.
6. W punkcie C3(3) nie chodzi o „reprezentatywne konstrukcje”, lecz o „typowe dla danego elementu konstrukcyjnego i dla danego stanu granicznego przypadki obciążeń i nośności”.
7. W punkcie C4(3) nie chodzi o „rzeczywistą proporcję konstrukcji ulegających zniszczeniu”, lecz o to, że procent realizowanych konstrukcji, które ulegają awarii, nie pokrywa się z prawdopodobieństwem awarii Pf przyjętym przy opracowywaniu norm.
8. Byłoby dobrze, gdyby przegląd metod kalibracji przedstawiony w rozdziałach C3 i C4 był mniej lakoniczny.
9. W punkcie C5(2) zamiast: „przy g>0 konstrukcja uważana jest za bezpieczną, a przy g≤0 – za niebezpieczną”, celowe byłoby napisać [6]: „gdy g>0, konstrukcja znajduje się w stanie bezpiecznym, gdy g = 0, konstrukcja znajduje się w stanie granicznym, gdy g<0, konstrukcja znajduje się w stanie niebezpiecznym, tzn. nastąpiło przekroczenie stanu granicznego – awaria”.
10. Punkt C5 zyskałby na przejrzystości, gdyby wzory (C.2a)÷(C.2e) zastąpić wzorami [1]:
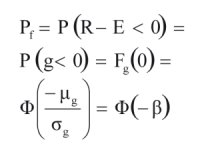 (1)
(1)
gdzie
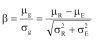
(2)
11. W rozdziale C6 budzi wątpliwości wzór (C.3)
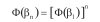
W przypadku zmiennej losowej X opisującej obciążenie zmienne w czasie, np. obciążenie śniegiem, zachodzi wprawdzie związek [6]
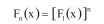 (3)
(3)
gdzie F1(x) oznacza dystrybuantę maksymalnych wartości odnotowanych w ciągu jednego roku, a Fn(x) – dystrybuantę maksymalnych wartości występujących w ciągu n lat, jednak wskaźnik β elementu konstrukcyjnego zależy nie tylko od rozkładu prawdopodobieństwa zmiennej opisującej losowość efektu obciążenia, ale także od zmiennej losowej opisującej jego nośność.
12. W punkcie C7(2) zamiast:
„…w punkcie obliczeniowym FORM, który może być zdefiniowany jako punkt na powierzchni zniszczenia (g = 0), najbliższy do średniego punktu w przestrzeni zmiennych losowych znormalizowanych”,
lepiej byłoby napisać [6]:
„…w punkcie projektowym, który zgodnie z metodą FORM definiuje się jako punkt na powierzchni stanów granicznych (g = 0) znajdujący się najbliżej początku układu współrzędnych zmiennych losowych standaryzowanych, czyli punktu, którego współrzędne w układzie zmiennych losowych początkowych odpowiadają wartościom średnim tych zmiennych”.
13. W punkcie C7 tzw. współczynniki wrażliwości nośności R i efektu obciążenia E, tj. αR i αE, proponuje się przyjmować równe odpowiednio –0,7 i 0,8 (s. 52), ewentualnie ±0,1 i ±0,4 (s. 53). Rezultatem tego są wzory (C7)÷(C9), a także wzory w tablicy C4 punktu C10. Tymczasem wartości αR i αE nie można dowolnie przyjmować, można je jedynie obliczać na podstawie odchyleń standardowych zmiennych losowych R i E. Definiuje się je bowiem jako tzw. cosinusy kierunkowe prostej stanu granicznego w układzie zmiennych losowych standaryzowanych R’ i E’ (ewentualnie stycznej do krzywej stanu granicznego w punkcie projektowym), czyli jako składowe wektora o długości równej 1, prostopadłego do tej prostej, poprowadzonego z punktu projektowego i skierowanego w kierunku obszaru awarii [6]. A zatem powinny one nie tylko spełniać warunek ?α?≤1, jak to padano w punkcie C7, ale także
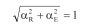 (4)
(4)
14. W tablicy C3 proponuje się odwracanie dystrybuanty zmiennej losowej dla prawdopodobieństwa p = Φ(–αβ), co jest niezgodne z przyjętą wcześniej metodą FORM.
15. Ponadto do wzorów, jakie zaproponowano na to odwracanie, wkradły się błędy. W przypadku zmiennej losowej o rozkładzie logarytmiczno-normalnym zamiast:
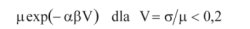
powinno być [6]:
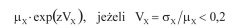 (5a)
(5a)
a
 (5b)
(5b)
gdzie
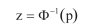 (5c)
(5c)
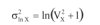 (5d)
(5d)
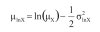 (5e)
(5e)
gdzie
μX i σX – odpowiednio wartość średnia i odchylenie standardowe zmiennej losowej X o rozkładzie logarytmiczno-normalnym.
W przypadku zmiennej losowej o rozkładzie Gumbela zamiast:
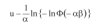
gdzie
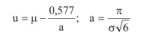
powinno być [6]:
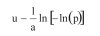 (6a)
(6a)
gdzie
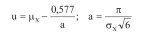 (6b)
(6b)
lub prościej:
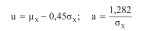 (6c)
(6c)
gdzie
μX i σX – odpowiednio wartość średnia i odchylenie standardowe zmiennej losowej X o rozkładzie Gumbela.
16. Użyty w punkcie C9 termin „oddzielne współczynniki częściowe” został użyty niefortunnie; chodzi tu prawdopodobnie o redukcję liczby częściowych współczynników bezpieczeństwa we wzorach projektowych formatu (5a) i (5b) przez ich wzajemne przemnożenie.
17. Dobrze byłoby, gdyby w całym załączniku C szczegółowo wyjaśniono różnicę pomiędzy trzema podejściami do projektowania opartego na rachunku prawdopodobieństwa:
– projektowanie na zadane prawdopodobieństwo awarii Pf, przy zastosowaniu wzorów projektowych formatu (4a) i (4b);
– projektowanie na zadane prawdopodobieństwo awarii Pf, przy zastosowaniu wzorów projektowych formatu (5a) i (5b);
– projektowanie na zadane prawdopodobieństwo przekroczenia wartości dopuszczalnych
i aby dla każdego z nich przedstawiono odpowiedni algorytm kalibracji częściowych współczynników bezpieczeństwa.
18. Dobrze byłoby, gdyby rysunek C2 – który nie w pełni jest poprawny, bo prosta stanu granicznego (a nie „granica zniszczenia”) g = R – E powinna być nachylona pod kątem 45° do osi R i E, ale nie do osi R/σR i E/σE, a ponadto wektor αR powinien być ujemny, a αE dodatni – zastąpiono ilustracją graficzną do wzorów (4a) i (4b) oraz (5a) i (5b), jak przedstawiam to na rysunku [5 i 6].
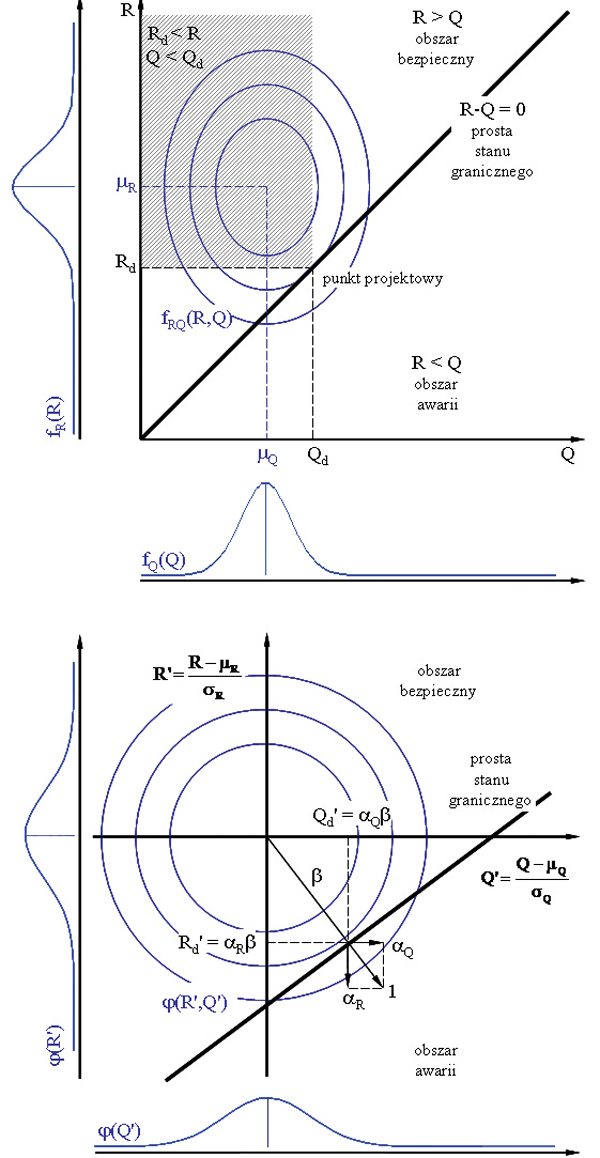
Rys. Interpretacja graficzna projektowania na zadane prawdopodobieństwo awarii oraz na zadane prawdopodobieństwo przekroczenia wartości dopuszczalnych w układzie zmiennych losowych R (nośność) i Q (efekt obciążeń) oraz w układzie zmiennych losowych standaryzowanych R’ i Q’
Uwagi końcowe
Tak jak Eurokody 1–9 powinny być gwarancją bezpiecznego projektowania konstrukcji, tak Eurokod Podstawy projektowania konstrukcji powinien być gwarancją prawidłowego opracowywania i aktualizowania Eurokodów 1–9. Powinien być „normą norm”.
Moim zdaniem Eurokod lepiej spełniałby to zadanie, gdyby przy jego opracowywaniu rozważono następujące kwestie:
– Czy konieczne jest, aby pojęcia i oznaczenia, do których przywykliśmy, zastępować nowymi, na przykład: „obciążenia” zastępować „oddziaływaniami”, a efekty tych „oddziaływań”, oznaczane dotąd przez Q (lub S), oznaczać przez E – symbolem, którym z kolei przywykliśmy oznaczać moduł Younga.
– Czy konieczne jest, aby w odniesieniu do pojęć, których znaczenie nie budziło dotąd wątpliwości lub było ustalone w Prawie budowlanym, wprowadzać nowe definicje, na przykład: „obiekty budowlane” definiować jako „wszystko to, co zostało zbudowane lub jest wynikiem robót budowlanych” (s. 9); „model obliczeniowy” definiować jako „idealizację ustroju konstrukcyjnego, stosowaną w celu analizy, wymiarowania i weryfikacji”(s. 10), a „zagrożenie” – jako „wyjątkowo niezwykłe i istotne zdarzenie” (s. 11).
– Czy nie należałoby postulaty, takie jak „konstrukcję należy zaprojektować tak, aby jej nośność, użytkowalność i trwałość były należyte” (s. 18) – równie słuszne, co ogólnikowe – zastąpić zwięzłym opisem spójnej metodologii projektowania i szczegółowymi procedurami kalibracji, które by je pozwoliły osiągnąć w praktyce.
Przydałoby się także dokonać ponownego opracowania polskiej wersji w celu uniknięcia:
– pomylenia niektórych pojęć, jak „własność materiału” z „wartością materiału” (s. 26); „wytrzymałość” – z „nośnością” (s. 48); „dystrybuantę” – z „funkcją rozkładu prawdopodobieństwa” (s. 50); „elektrownie atomowe” – z „instalacjami nuklearnymi” (s. 8);
niekonsekwencji w przyjętej terminologii, zastępowanie „projektowego okresu użytkowania” (zdefiniowanego na s. 11) „przewidywanym okresem użytkowania” (s. 11) lub „zamierzonym okresem użytkowania” (s. 18);
– niefortunnych sformułowań, jak: „konstrukcje zwykłe” (s. 20) i „odmienne od zwykłych” (s. 6), „modelowanie modelu materiału” (s. 7), „miarodajna wartość reprezentatywna” (s. 17), „dokument wiodący przewodni”(s. 7), „dobór ustroju konstrukcyjnego i takie jego zwymiarowanie, aby mógł odpowiednio przetrwać utratę na skutek wypadku pojedynczego elementu lub pewnej części konstrukcji” (s. 18) albo „β niekoniecznie zawiera wskazanie o rzeczywistej częstości zniszczenia konstrukcji” (s. 51) itp.
Jednym słowem może Eurokod Podstawy projektowania konstrukcji powinien zostać opracowany ponownie, zarówno pod względem merytorycznym, jak i redakcyjnym.
dr inż. Ewa Szeliga
Wydział Inżynierii Lądowej
Politechniki Warszawskiej
Literatura
1. PN-EN 1990:2004 Eurokod – Podstawy projektowania konstrukcji, 2004.
2. EN 1990:2002 Eurocode – Basis of structural design, 2002.
3. Building Code Requirements for Structural Conrete (ACI 318-05) and Commentary (ACI 318R-05), An ACI Standard.
4. B. Ellingwood, T.V. Galambos, J.G. MacGregor, C.A. Cornell, Development of Probability Based Load Criterion for American National Standard A58, NBS Special Report 577, US Department of Commerce, National Bureau of Standards, 1980.
5. J. Murzewski, Niezawodność konstrukcji inżynierskich, Arkady, Warszawa 1989.
6. A.S. Nowak and K.R. Collins, Reliability of Structures, McGraw-Hill, New York 2000.
7. A.S. Nowak, E.K. Szeliga and M.M. Szerszen, Statistical Models for Resistance of Concrete Components, Proceedings of the 12th WG 7.5 Working Conference on Reliability and Optimization of Structural Systems, Aalborg, Denmark 2005, pp. 171–178.
8. A.S. Nowak, E.K. Szeliga and M.M. Szerszen, Reliability-Based Calibration for Structural Concrete, Proceedings of the 5th Int. Conference on Analytical Models and New Concepts in Concrete and Masonry Structures, Ustroń, Poland, June. 2005, CD ROM.
9. A.S. Nowak, M.M. Szerszen, E.K., Szeliga A. Szwed and P.J. Podhorecki, Reliability–Based Calibration for Structural Concrete, Report No. UNCLE 05-03, University of Nebraska, October 2005.
10. A.S. Nowak, E.K. Szeliga and M.M. Szerszen, Reliability-Based Calibration of Design Code for Concrete Structures, Proceedings of the RILEM–JCI Seminar, Ein-Bokek, Israel, March 2006, pp. 341–350.
11. A.S. Nowak and E.K. Szeliga, Resistance Factor for Structural Plain Concrete, Report for ACI 318C (American Concrete Institute) Committee, ACI Fall 2006 Convention, November 5–9, Denver.